Inscription / Connexion Nouveau Sujet
étude d'un systeme du second d'ordre
Bonjour à tous(tes)
j'ai un petit probleme de physique sur un systeme du second ordre !
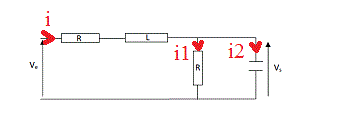
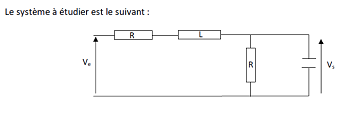
J'ai joint une photo du systeme !
On me demande de trouver la fonction de transfert H(p) : j'ai joint la réponse en détail
Désormais , (je ne sais pas si la fonction de transfert est bonne) je bloque sur cette question :
on prend L=10mH et C=10 F;
F;
trouver les différentes valeurs que R peut prendre (il y en a trois: pour régime critique, apériodique, semi périodique).
je pensais par exemple poser :
z=1 j'appelle z le coefficient de frottement 
z<1
z>1
mais je n'arrive pas à aboutir
Si des âmes éclairées pouvaient m'aider où bien m'éclaircir le chemin, ce serait charitable
Cordialement chères collègues
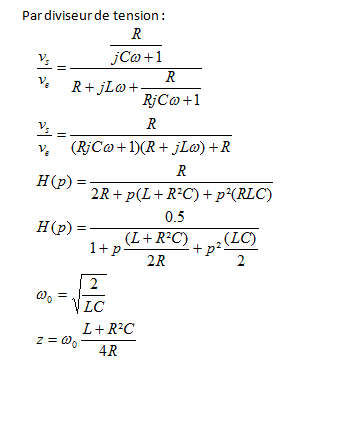
Bonjour xxAlPhAT3AMxx,
la fonction de transfert H( ) = Vs/Ve (rapport des amplitudes de ces deux tensions) s'applique a un circuit electrique en regime permanent sonusoidal de pulsation
) = Vs/Ve (rapport des amplitudes de ces deux tensions) s'applique a un circuit electrique en regime permanent sonusoidal de pulsation  ; la notion de resistance crituque concerne un circuit soumis a un regime transitoire. Curieux melange !
; la notion de resistance crituque concerne un circuit soumis a un regime transitoire. Curieux melange !
Ta fonction de transfert est evidemment fausse, car le passage de la ligne 2 (vs/ve complexes) a la ligne 3 (H( )) est fait au mepris des regles elementaires de calcul algebrique faisant intervenir l'imaginaire j.
)) est fait au mepris des regles elementaires de calcul algebrique faisant intervenir l'imaginaire j.
Voici les etapes du calcul concernant la recherche de la fonction de transfert :
On pose Z1 = R + jL , Z2 = R/(1 + jRC
, Z2 = R/(1 + jRC ).
).
Vs/Ve = Z2/(Z1 + Z2) = R/[R + (R+jL )(1 + jRC
)(1 + jRC )], les grandeurs soulignees Ve et Vs representant les images complexes des deux fonctions sinusoidales ve(t) et vs(t).
)], les grandeurs soulignees Ve et Vs representant les images complexes des deux fonctions sinusoidales ve(t) et vs(t).
L'expresion ci dessus donne la fonction de transfert complexe H(j ). Il faut en extraire le module pour obtenir H(
). Il faut en extraire le module pour obtenir H( ), cad le rapport des amplitudes Vs/Ve. On obtient H(
), cad le rapport des amplitudes Vs/Ve. On obtient H( ) = R/
) = R/ [(2R - LC
[(2R - LC 2)2 + (L
2)2 + (L + R2C
+ R2C 2)].
2)].
On verifie que H( ) tend vers 1/2 si
) tend vers 1/2 si  tend vers 0, et vers 0 si
tend vers 0, et vers 0 si  tend vers l'infini, ce qu'on pouvait obtenir sans calcul.
tend vers l'infini, ce qu'on pouvait obtenir sans calcul.
Concernant l'etude du meme circuit en regime transitoire, en supposant que la tension d'alimentation et une fonction creneau passant brutalement a l'instant initial de la valeur 0 a la valeur E constante. La tension v(t) aux biornes de C verifie l'equation differentielle LC.d2v/dt2 + (L/R + RC).dv/dt + 2v = E
Le discriminant de vette equation s'annule pour une valeur particuliere Rc de R telle que Rc2 = (L/C).(3 +  8)
8)  5.83L/C. Pour R > Rc le regime est aperiodique (double exponentielle partant de 0 pour arriver vers E), et pour R < Rc le regime est pseudo-periodique.
5.83L/C. Pour R > Rc le regime est aperiodique (double exponentielle partant de 0 pour arriver vers E), et pour R < Rc le regime est pseudo-periodique.
Prbebo.
xxAlPhAT3AMxx, je ne suis pas sur a 100% de la valeur de Rc donnee dans mon post precedent. Je viens de me rappeler que j'ai deja fait cet exercice a mes etudiants dans le cas particulier ou L, C et R sont relies par la relation L/R = RC = 
desole, mon ordi a encore envoye mon message avant sa fin. Je te disais que quand L, C et R sont tels que L/C = R2, on arrive a une equation differentielle dont le discriminant est toujours negatif, donc fournissant un regime pseudo-periodique. Dans le cas de ton exo ou cette condition n'est pas imposee, j'aurais du pourtant la faire apparaitre. Sans doute fais-je une erreur, sinon de calcul, du moins de raisonnement : je vais revoir ca demain.
De ton cote, renseigne-toi pour savoir si ton circuit est alimente par un generateur sinusoidal (donc en regime permanent sinusoidal), ou si on etudie "simplement" son regime transitoire. Et tiens-moi au courant de la reponse, et accessoirement dis-moi ce que veut dire "CDLMT".
Prbebo.
Bonsoir,
cordialement veut dire cdlmt
je ne sais pas si le circuit est alimenté par un generateur sinusoidale, mais je sais qu'ensuite, je dois étudier le systeme en régime transitoire sous simulink.
Cordialement
j'ai une autre question,
comment passer de h( ) à h(p)
) à h(p)
et comment faire pour retrouver la même équation avec les formules non complexes ?
POUR SYNTétiser;
je ne vois pas pourquoi on travaille avec le module de H(j ) puisque l'on me demande en fonction de p .
) puisque l'on me demande en fonction de p .
de plus, je ne sais pas retrouver une équation de ce type en régime transitoire, (sans les j ), car je ne vois pas quel est l'équivalent de R
), car je ne vois pas quel est l'équivalent de R C
C
et enfin, je crois que je dois faire l'étude en régime transitoire
cordialement (=cdlmt)
Bonsoir xxAlPhAT3AMxx,
je n'ai pas trop le temps de te repondre maintenant, mais plutot demain en fin d'apres-midi.
"cordialement veut dire cdlmt" : personnellement j'aurais plutot dit l'inverse, mais bon. L'essentiel est de se comprendre.
"comment passer de h( ) à h(p)" : le tout est de savoir ce que c'est que p. Moi j'ai cru que c'etait l'initiale de "pulsation", donc pour moi H(p) et H(
) à h(p)" : le tout est de savoir ce que c'est que p. Moi j'ai cru que c'etait l'initiale de "pulsation", donc pour moi H(p) et H( ) c'est la meme chose. Si je me trompe, dis-moi ce que veut dire p.
) c'est la meme chose. Si je me trompe, dis-moi ce que veut dire p.
"et comment faire pour retrouver la même équation avec les formules non complexes ?" : la meme equation que quoi ? Si c'est celle que j'ai donnee (le rapport Vs/Ve), de toutes facons la reponse est : impossible. Seule la notation complexe permet de traiter un circuit en regime permanent sinusoidal comme s'il etait alimente en regime permanent continu.
"je ne vois pas pourquoi on travaille avec le module de H(j ) puisque l'on me demande en fonction de p" : je te repondrai lorsque j'aurai compris la difference entre
) puisque l'on me demande en fonction de p" : je te repondrai lorsque j'aurai compris la difference entre  et p.
et p.
"je ne sais pas retrouver une équation de ce type en régime transitoire, (sans les j )" : j'ai l'impression que tu n'as pas compris a quoi sert la notation complexe.
)" : j'ai l'impression que tu n'as pas compris a quoi sert la notation complexe.
"enfin, je crois que je dois faire l'étude en régime transitoire" : Ca, oui ! Et pour ca il faut connaitre les relations tension-courant pour une inductance L et pour un condensateur C.
*) pour une inductance L : VA - VB = L.di/dt ;
*) pour un condensateur C : i = dq/dt = C.dv/dt.
On reprend l'exercice demain.
Prbebo.
Z1 = R//C
Z1 = (R/pC)/(R + 1/pc) = R/(1+pRC)
Z2 = R série L
Z2 = R + pL
Vs/Z1 = Ve/(Z1 + Z2)
Vs/Ve = Z1/(Z1 + Z2)
H(p) = [R/(1+pRC)]/[R/(1+pRC) + R + pL]
H(p) = R/(R + (R+pL)(1+pRC)]
H(p) = R/(2R + p(L+R²C) + p²LRC)
H(p) = (1/2)/(1 + p.(L+R²C)/(2R) + p²LC/2)
-----
H(p) 1/(1 + 2p.Zeta/wo + p²/wo²)
--->
wo = V(2/(LC))
Zeta = V(2/(LC)) * (L + R²C)/(4R)
Régime critique si Zeta = 1
V(2/(LC)) * (L + R²C)/(4R) = 1
R = V(L/C) * (V2 +/- 1)
R = V(10^-2/10^-5) * (V2 +/- 1)
R = 13,1 ohms et R = 76,3 ohms.
---
Régime périodique si Zeta < 1
Donc pour 13,1 < R < 76,3 ohms
---
Régime apériodique si Zeta > 1
Donc pour 0 < R < 13,1 ohms ou R > 76,3 ohms.
-----
Sauf distraction. 
bonjour,
dans votre dernière ligne de h(p), il me semble que vous ayez oublié un "1/2" au numérateur, sauf si je me trompe
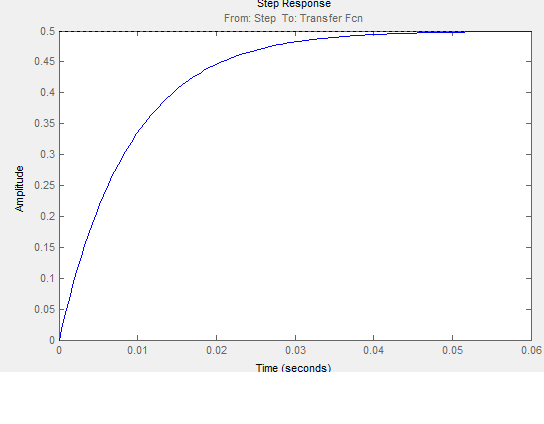
en tout cas je trouve pareil que toi il me semble ! je poste la photo si tu peux me dire si j'ai bon  ? en tout cas un grand merci à voous
? en tout cas un grand merci à voous
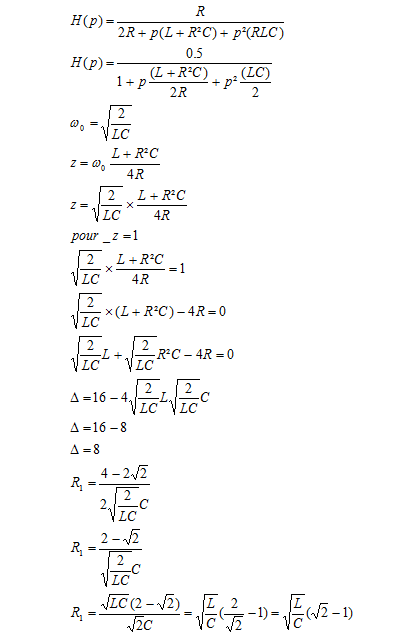
Merci,
juste une petite question, pour le régime périodique, c'est entre les deux racines, comme en mathématiques ?
Le régime périodique, c'est pour Zeta < 1 et donc pour les intervalles de valeurs de R pour lesquels on a : V(2/(LC)) * (L + R²C)/(4R) < 1
Les mathématiques ne sont qu'un outil qui permet de trouver ces intervalles.
Il suffit donc d'étudier le signe de f(R) = V(2/(LC)) * (L + R²C)/(4R) - 1
Par la méthode classique étudiée au cours de Math ou par toute autre méthode licite.
... Et ensuite d'en tirer les conclusions.

et une dernière question si ce neest pas trop vous demander :
en passant par les valeurs instantannées, je voudrais retrouver la même équation, mais je suis confronté au problème suivant :
pour Z1 on a Z1=R+Ldi/dt
pour Z2 on a Z2=C R mais je ne vois pas à quoi c'est égal. je ne trouve pas quel est son équivalent.
R mais je ne vois pas à quoi c'est égal. je ne trouve pas quel est son équivalent.
je ne pense pas que (R*C*du/dt)/(R+C*dU/dt) soit la bonne formule ? je ne vois pas comment procéder.
si vous pouviez m'indiquer juste le début pour savoir et je dévellopperai moi même par la suite
cordialement
[img1]
Ve - R.i - L.di/dt - Vs = 0
i1 = Vs/R
i2 = C.dVs/dt
i = i1 + i2
i = Vs/R + C.dVs/dt
Ve - R.(Vs/R + C.dVs/dt) - L.d(Vs/R + C.dVs/dt)/dt - Vs = 0
Ve - Vs - RC.dVs/dt - L/R .dVs/dt - LC.d²Vs/dt² - Vs = 0
LC.d²Vs/dt² + (RC + L/R).dVs/dt + 2Vs = Ve
LRC.d²Vs/dt² + (R²C + L).dVs/dt + 2R.Vs = Ve.R (1)
Qui est évidemment équivalent à ce qui a été trouvé avant, en effet :
En remplaçant p par d/dt dans l'expression trouvée précédemment pour H(p) = R/(2R + p(L+R²C) + p²LRC)
Vs/Ve = R/(2R + p(L+R²C) + p²LRC)
(2R + p(L+R²C) + p²LRC).Vs = R*Ve
abec p --> d/dt et pa --> d²/dt², on a :
2R.Vs + (L+R²C).dVs/dt + LRC.d²Vs/dt² = R.Ve
qui est la relation (1) trouvée avant.
dernière petite question.
est-il nécessaire de connaitre les valeurs de R pour tracer les courbes ?
personnelement je ne pense pas puisque l'on pose z=1
je ne sais pas si vous connaissez simulink?
en utilisant des valeurs plutôt particulière par exemple 447.10-7 pour 2z/w0 je trouve une courbe de réponse particulièrement interressante . comment puis-je choisir des valeurs concretes.
par exemple, pour R=13.1, 76.1, 20, 100, 1 , on trouve des courbes de réponses avec un temps de réponse plus ou moins rapide.
me serai-je tromper?
voila l'image que j'ai
je dois partir dans des valeurs trés élevée ou très faible pour obtenir les courbes caractéristiques des régimes pseudo périodiques et peu amortis
cordialement