Inscription / Connexion Nouveau Sujet
Etude d'un sismographe
Bonjour
Voici l'énoncé de mon exercice :
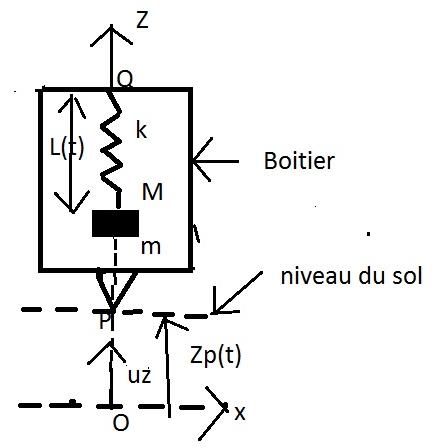
On considère le dispositif représenté sur la figure ci-dessous : un boîtier (B) muni d'une pointe P est posé sur le sol, de telle sorte que sa pointe suive les déplacements verticaux du sol, repérés dans un référentiel galiléen (R) par leur côte Zp(t) sur la verticale ascendante  z . Les axes Ox et Oz sont liés à ce référentiel (R). En présence d'une onde sismique le niveau du sol peut se déplacer verticalement par rapport au référentiel R.
z . Les axes Ox et Oz sont liés à ce référentiel (R). En présence d'une onde sismique le niveau du sol peut se déplacer verticalement par rapport au référentiel R.
Les extrémités Q et M d'un ressort de raideur k et de longueur à vide Lo sont fixées respectivement au boîtier et à un point matériel de masse m. La position de M par rapport au boîtier est repérée par la longueur L(t) du ressort.
Le mouvement de la masse m est amorti par une force F= f*dL/dt  z=, où f est une constante positive. F un vecteur
z=, où f est une constante positive. F un vecteur
1) En l'absence d'onde sismique, le point P est fixe : Zp(t) = 0. Exprimer la longueur L1 du ressort lorsque la masse m est en équilibre, en fonction de Lo, m, g et k.
Cette question j'ai réussi mais je voudrais savoir si c'est juste?
A l'équilibre la sommes des forces extérieures s'annulent
-mg z+k(L1-L0 )=0
z+k(L1-L0 )=0
L1= (mg+k*L0)/k
[b]2) Dans toute la suite, on pose L(t) = L1 - z(t) et on suppose que l'électronique du sismographe permet d'obtenir directement z(t).
Exprimer l'accélération du point M dans R en fonction de d2Zp/dt2 et d2z/dt2 .[/b]
C'est pour cette question que je suis bloquée
Je sais qu'il faut écrire la relation fondamentale de la dynamique appliquée au solide dans le référentiel lié au boîtier (avec le poids la tension du ressort)
Mais quand j'ai regardé sur le net on ajoute 1 terme que je ne comprend pas -m*d2z/dt2  z
z
Et pour la force F je ne sais pas dans quel sens est elle dirigée ?
Désolé pour le dessin un peu brouillon mais je n'ai pas de scanner chez moi
Merci d'avance pour les personnes qui prendront le temps de me répondre.

bonjour,
dans la question 2) on te demande juste d'écrire la composition des accélérations si j'ai bien compris l'énoncé
 a(M) =
a(M) =  r +
r +  e +
e +  c
c
 e = Z"P
e = Z"P
 r = ...
r = ...
 c = ...
c = ...
Et j'ai vu que lorsque que l'on a un référentiel R non galiléen la deuxième loi de Newton s'exprime de cette manière (et en utilisant la decomposition des accélérations )
m*aR=F-m*ae-m*ac= F+fie+fic
Je n'arrive pas à voir comment vous écrivez  e = Z"P
e = Z"P
PS: Je voulais vous préciser que je n'ai pas eu de cours à proprement dit en physique donc le cours je me le fait un peu toute seul avec ce que je vois sur le net et les bouquins .
Ah d'accord donc la question 1 le système c'est la masse +ressort qui Et ce système est dans un référentiel Galiléen
Et dans la 2 le système est le boitier (c'est à dire masse+ressort+pointe) et ce boitier a un mouvement accéléré par rapport au sol (qui est galiléen)
Donc le système que l'on étudie est dans un référentiel est non galiléen
C'est bien ça ?
Et encore une question je ne vois pas comment représente la force F évoquée dans l'énonce ?
Merci du temps que vous m'accordez pour me répondre 
le système étudié ici est la masse M
dans le 2) on peut calculer a(M)/R en passant par un référentiel lié à B:
accélération absolue = accélération relative + accélération d'entrainement + accélération de Coriolis
 F = m a(M)/R = m(ar+ae + ac)
F = m a(M)/R = m(ar+ae + ac)
a(M)/R = (ar+ae + ac) = a(M)/B + Z"p + 0
et a(M)/B = z"
sauf erreur
la force F s'oppose au mouvement de M (càd à sa vitesse)
si M va vers le bas, F est orientée vers le haut et inversement
F = -fz'  z
z
Pour la question 2
Quand j'écris la RFD dans le referentiel non galileen
J'obtiens ceci mais je ne suis pas sure du tout  :?
:?
 Fext=m*a/R1 R1 non galileen
Fext=m*a/R1 R1 non galileen
P+T+F+Fie=m*dz2/dt2
Fie force d'inertie d'entrainement car referentiel non galileen
-mg+k(L1-L0)+fdZ/dt=mdz2/dt2
tu as calculé l'accélération absolue donc tu peux travailler dans R:
(en projetant sur  z)
z)
m(z" + Z"P) = -mg + k(L-Lo) -fz'
avec L = L1-z
si tu veux travailler dans le repère lié à B non galiléen, tu retrouves la même chose:
mz" = -mg + k(L-Lo) -fz' + Fie + Fic
avec Fie = -mZ"P et Fic=0
le terme -mg + k(L-Lo) se simplifie en utilisant les relations:
L = L1-z
et
mg = k(L1-L0) (trouvé en 1)
sauf erreur
Je vous remercie infiniment Krinn pour l'aide que vous m'avez apporté à cet exercice , j'ai donc pu facilement le terminer
Mais il y a point qui n'est pas très clair concernant l'accélération
Je n'arrive pas à faire la différence entre l'accélération absolue et relative
Quand vous écrivez :
accélération absolue = accélération relative + accélération d'entrainement + accélération de Coriolis
l'accélération absolue est l'accélération dans un référentiel R galiléen
et la relative dans un autre référentiel non galiléen

oui,
il est souvent plus simple de travailler dans un repère intermédiaire qui n'est pas galiléen (par ex. un repère accéléré comme ici le repère lié à B, ou encore un repère tournant)
en effet ici la position de M dans B est simplemenent donnée par L = L1 - z
si on voulait repérer M dans R, il faudrait faire intervenir la hauteur de la boîte etc.
donc l'accélération relative à B est simple, ici c'est: ar(M) = z" z
z
il y a juste un problème: la loi de Newton ne s'applique pas directement dans B
2 variantes:
a) tu calcules l'accélération absolue dans un repère galiléen (ici R) avec la formule de composition et tu appliques la loi de Newton dans R
ici, tu trouves: m(z" + Z"P +0) = -mg + k(L-Lo) -fz'
b) tu appliques, dans B, une variante de la loi de Newton qui tient compte des "forces" d'inertie (et qui s'applique aux repères non galiléens)
ici, mz" = -mg + k(L-Lo) -fz' -mZ"P + 0
c'est équivalent, il faut juste ne pas se tromper dans les signes: Fie = -mae Fic = -mac
dans tous les cas, tu dois calculer ae et ac pour trouver soit l'acc. absolue , soit les forces d'inertie selon la variante utilisée


