Inscription / Connexion Nouveau Sujet
Etude d'un saut de ravin avec une petite voiture
Bonjour,
Je suis actuellement étudiant en prépa, mais je suis pas très bon en mécanique et j'ai besoin d'un peu d'aide sur un exercice que je dois rendre bientôt. L'exercice resemble à ça:
"La voiture doit faire un saut au dessus d'un ravin.
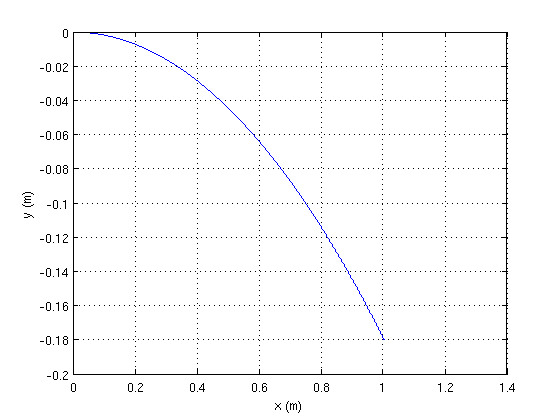
L'objectif est de déterminer la vitesse minimale nécessaire au franchissement du ravin sans encombre. La voiture devra atteindre un point donné K de coordonnées (1m ;-0,18m) pour atterrir en toute sécurité.
Dans un premier temps, les calculs seront effectués sans frottements puis avec les frottements de l'air.
Le livrable demandé est une note de calculs qui comprendra :
I) Les équations du mouvement de la voiture lâchée avec une vitesse initiale sans puis avec frottements (la résolution devra se faire par une méthode numérique à l'aide de Scilab et Euler)
II) La valeur de la vitesse minimale à avoir pour franchir le ravin de longueur L=1m.
III) Une étude de la variation des différents paramètres sur le résultat de la vitesse à l'aide de Scilab"
L'image attachée montre le schéma du ravin (après le looping) et de l'élan que va prendre la voiture, ainsi que sa masse.
J'ai fait une méthode sur Scilab qui permet de calculer une équation différentielle ordinaire avec des paramètres initiaux mais j'ai aucune idée de comment elle peut m'aider à résoudre l'exercice. J'ai aussi fait le calcul de la vitesse sans frottements
Merci d'avance pour votre aide.
Bonjour et bienvenu sur ce forum.
Tu ne précises pas si la vitesse initiale est un vecteur horizontal.
Comment modélises-tu la force de frottement ? Peut-être quelque chose de la forme suivante :
?
Ton programme sous Scilab ou autre logiciel permet d'obtenir la trajectoire. En augmentant progressivement la valeur de la vitesse initiale, il va t'être facile de voir à partir de quelle vitesse, la voiture passe en y=-0,18m pour x 1m.
1m.
Si tu veux, indique ici tous les paramètres que tu utilises dans ta simulation et indique ton résultat. On pourra comparer avec mes résultats...
Le message précédent a été écrit avant que ton schéma n'apparaisse sur le forum. Cette figure me gêne un peu : assimiler le véhicule à un point matériel n'a de sens que si les dimensions du véhicules sont petites devant les autres dimensions du problème. Or, le rayon de la piste circulaire n'est que de 11,5cm soit l'ordre de grandeur de la longueur de la voiture ! Je préférerais imaginer un petit glaçon qui glisse sans frottement sur la piste avant de "sauter" au-dessus du ravin.
La modélisation de l'influence des frottements dus à l'air n'est pas simple dans le cas de la trajectoire circulaire.
Tout d'abord, merci pour votre aide.
La trajectoire à étudier est seulement celle du ravin, après le looping. J'imagine que la vitesse initiale est un vecteur horizontal à cet instant là, non?
Voici le programme scilab réalisé :
__________________________________________________________________________________________
clear()
//Déclarer les variables et les fonctions nécessaires au calcul :
v0=5
alpha=0*%pi/180
tfinal=10
//On veut trouver x'(t) et y'(t) grâce à x''(t) et y''(t) grâce à la fonction ode résolution d'une équation différentielle linéaire du 1er ordre.
// déclaration de la fonction x'' en fonction de x' et t
function xpp=f(t, xp)
xpp=0
endfunction
// déclaration des conditions initiales et du pas de temps de calcul (t varie de 0 à Pi par pas de 0.1s)
xp0=v0*cos(alpha);
t0=0;
t=0:0.1:%pi;
// résolution de l'équation différentielle
xp=ode(xp0,t0,t,f);
plot2d(t, xp);
a=gca();
a.title.text='Vitesse de la voiture';
a.x_label.text='Temps (s)';
a.y_label.text='Vitesse (m/s)' ;
// déclaration de la fonction y'' en fonction de y' et t
function ypp=f(t, yp)
ypp=-9.81
endfunction
// déclaration des conditions initiales et du pas de temps de calcul (t varie de 0 à Pi par pas de 0.1s)
yp0=v0*sin(alpha);
t0=0;
t=0:0.1:%pi;
// résolution de l'équation différentielle
yp=ode(yp0,t0,t,f);
plot2d(t, yp);
_____________________________________________________________________________________________
J'imagine que la vitesse initiale est un vecteur horizontal à cet instant là, non?
oui d'après le schéma fourni.
Si je comprends bien, tu te limites pour l'instant à l'étude en absence de frottement. Inutile d'utiliser une simulation dans ce cas. Il est facile de trouver que la trajectoire est alors une branche de parabole. Tu obtiens la valeur minimale de Vo en écrivant que la parabole doit passer par le point de coordonnées (1,-0,18) en mètres.
La simulation numérique est intéressante pour tenir compte des frottements. Peux-tu copier ton code dans ce cas ?
Bonjour,
Merci encore pour votre aide 
Pardon, mais... Copier mon code? C'est à dire? Je l'ai déja posté en réponse hier, mais ce n'est pas ça qu'il faut?
Si je comprends bien ton code, tu t'es contenté de l'étude en absence de frottement. Franchement, pour une étude aussi simple, la théorie conduit très simplement au résultat.
En choisissant comme origine du repère, le point où le véhicule quitte le sol :
x=Vo.t
y=-½g.t2
Facile d'obtenir la date t1 correspondant à y=-0,18m. Il suffit alors de considérer que le ravin est franchi en toute sécurité si : x1=Vo.t1>L ; à toi de vérifier : selon moi, cela correspond à Vo 5,2m/s
5,2m/s
En revanche, Scilab devient très intéressant dès qu'on tient compte des frottements qui modifient l'expression de l'accélération. Je t'ai proposé une modélisation possible mais on peut en envisager d'autre. Relis bien mes messages précédents.
Petite remarque : la procédure "ode" de scilab utilise une méthode de résolution de l'équation différentielle plus sophistiquée que la simple méthode d'Euler. Te faut-il utiliser la précédure "ode" ou te faut-il programmer la méthode d'Euler ?
Comme dit dans mon message précédent, en absence de frottement, sans utiliser l'informatique mais seulement les équations du mouvement, j'ai obtenu Vo 5,2m/s.
5,2m/s.
En présence de frottement, il faut trouver certainement une valeur un peu supérieure de Vo. Avant de t'aider davantage sur la programmation, il faudrait que tu m'en dises plus sur la modélisation des frottements. Je t'ai proposé une modélisation dans mon message du 06-03-19 . Pour une voiture réelle, c'est à mon avis la plus réaliste mais, comme il s'agit ici d'un jouet et de vitesses très faibles, on peu en imaginer d'autres un peu plus simples.
Quel modèle adoptes-tu et en quoi cela change-t-il ton programme ?
J'ai ressorti une voiture miniature de ma réserve. J'ai mesurée :
masse : m = 35.10-3kg
En reprenant les notations de mon message du 6/03/19 à 13h56 :
Surface frontale S=6cm2=6.10-4m2
masse volumique de l'air dans les conditions ambiantes :
Coefficient d'aérodynamisme : Cx=0,3
Cela me conduit à :
La projection sur les deux axes de la relation fondamentale de la dynamique conduit à :
Avec pour conditions initiales :
Tu peux alors intégrer en utilisant la méthode d'Euler ou la procédure « ODE » de SCILAB.
Je viens de programmer la méthode d'Euler sous Matlab avec les valeurs numériques précédentes. A ces faibles vitesses, les frottements dus à l'air sont relativement faibles. En imaginant l'absence de frottement, on obtient comme déjà dit : Vo 5,2m/s
5,2m/s
La simulation précédente avec frottement conduit à : Vo 5,3m/s.
5,3m/s.
Je pense que, lors des étapes précédentes du mouvement, les frottements prépondérants sont les frottements solides entre l'axe des roues et le châssis. Coup de chance, de tels frottements peuvent se modéliser par une force d'intensité constante.
vanoise je peux voir ton code pour essayer de comprendre s'il te plaît, je n'arrive pas a le faire sur scilab :/
Je t'ai fourni les équations différentielles à résoudre puisque je t'ai fourni les expressions des accélérations suivant x et suivant y.
J'ai l'habitude d'utiliser Matlab ou même un simple tableau comme Excel ou LibreOffice. Je ne connais pas Scilab.
Tu trouveras ici, partie IV, paragraphes 1 et 2, la méthode d'Euler expliquée pour une situation analogue. Il te suffit de remplacer les expressions des accélérations par celles fournies dans mon message du 12-03-19 à 18:50.
![]()
Bonjour,
J'ai un sujet similaire et je pense avoir réussi cependant les profs m'ont mis un doute. De ce fait; pourriez vous m'envoyer votre correction sur mon mail: fadi.wihbeh@hotmail.fr.
Merci
Bonjour Fadiw34
Bienvenu sur ce forum tout d'abord ! 
pourriez vous m'envoyer votre correction sur mon mail
Ce n'est pas comme cela que fonctionne ce forum. Tu peux poster ici une proposition de code Scilab ou autre dans le cas du mouvement avec frottement. Il sera alors possible de le corriger ou de l'améliorer si nécessaire.
Bonjour,
pouvez vous nous envoyer votre livrable par rapport à ce projet s'il vous plaît?
Nous avons du mal à le réaliser et en avons vraiment besoin.
Bien à vous.
Merci de votre compréhension.
Bonjour,
J'ai le même exercice et je voudrais savoir comment je pourrais résoudre ces 3 problèmes:
-I) La résolution des équations du mouvement de la voiture avec frottements (la résolution devra se faire par une méthode numérique à l'aide de Scilab et Euler).
-II) Le calcul de la vitesse d'entrée nécessaire pour faire le tour du looping avec frottements.
-III) Le calcul de la vitesse de sortie du looping avec frottements.
Mon problème vient des frottements, j'ai déjà les calculs sans frottements.
Si quelqu'un a une idée je suis preneur.
Bonjour
L'essentiel est expliqué dans mon message du 12 mars 18h50. Tu y trouves les équations différentielles à résoudre numériquement.
bonjours, j'ai moi aussi le meme probleme j'ai pu faire en premier le Pfd avec frottement de l'air que j'ai pris comme (frottement quadratique) plus le poids =ma, ensuite j'ai de essayer de resoudre l'equation a sont maximum et donc je suis bloquer a ca :
-v'+g -(1/2m)*rho*coef de trainée*surface*v²*le pas choisit
je rappelle que je cherche a determinée la vitesse minimal que doit faire la voiture pour passer le ravin et je suis bloquer la je sais pas quoi faire un sciilab ? un tableur ?
si quelqu'un peut m'aider rapidement svp
C'est exactement ce qui a déjà été fait ici : les projections de l'équation vectorielle sur les deux axes sont dans mon message du 12-03-19 à 18:50.
Pour tenir compte de la force de frottement ayant la direction et le sens de , tout en ayant une norme proportionnelle au carré de la norme de la vitesse, je l'ai écrite sous la forme :
Si tu veux utiliser la méthode d'Euler, un simple tableur suffit comme cela a été expliqué ici, paragraphe IV, pages 6 et suivantes :
![]()
Des logiciels comme Scilab ou Matlab utilisent des procédures plus sophistiquées et précises (méthode de Runge Kutta...). Le code est très facile à saisir.. Tu peux faire ici une proposition de programme.
L'énoncé initial demande de déterminer la valeur de Vo pour obtenir le passage par un point de coordonnées (x=1,00m,y=-0,18m). Le plus simple consiste à calculer la valeur théorique de Vo permettant le passage par ce point pour une trajectoire parabolique en absence de frottement : Vo=5,22m/s. A partir de cette valeur, on procède par "talonnements", sachant que la valeur à trouver n'est que de très peu supérieure à cette valeur.
merci de votre réponse, alors en effet je compte utiliser la methode d'Euler et donc un tableur, mais j'ai encor plusieurs question (désoler je ne suis pas tres bon en meca)
reprenez moi si j'ai faux mais si j'ai bien compris a partir de mon equation du dessus je peux faire les equation vectoriel sur x et y trouver au dessus ?
ensuite quel pas prendre pour mon etude ?
j'ai donc déjà auparavant trouvée la valeurs qu'il fallait pour passer sans frottement = 4.9m.s
ensuite que veux dire procéder par talonnement ?
voici les donnée de mon exercice : coef de trainer = 1.05
rho = 1,225
masse voiture = 0.03kg
surface voiture = 4.69cm²
Si tu projettes sur les deux axes la relation vectorielle traduisant la relation fondamentale de la dynamique :
tu obtiens les deux équations fournies dans mon message du 12-03-19 à 18:50. A toi de refaire les applications numériques. Un coefficient de traînée Cx=1,05 : cela est vraiment beaucoup ! il s'agit quasiment de celui d'une plaque orientée perpendiculairement au vecteur vitesse de son centre de gravité : pas très aérodynamique comme situation ! Les voitures actuelles de tourisme ont un Cx compris entre 0,3 et 0,4, les voitures de sport ayant un Cx encore plus faible.
La méthode d'Euler demande un pas de calcul assez faible pour être précise. Ici, tu peux commencer par évaluer ce que serait la durée du mouvement en absence de frottement et choisir un pas d'environ le centième de cette valeur.
Remarque : choisir un Cx élevé à cependant un avantage : on voit très clairement la différence entre le mouvement parabolique sans frottement et le mouvement avec frottement. Sion, sur un parcours aussi court, la différence de trajectoire ne serait pas significative.
En absence de frottement, on obtient avec tes valeurs numériques : Vo=4,90m/s (pas m.s !)
Bonjour
Dans votre message du 12-03-19 à 18:50, je ne comprend pas comment utiliser la projection de l'accélération dans Euler. J'ai bien regardé le lien que vous nous avez donnés mais je ne vois pas aussi comment il passe de la projection à l'équation différentielle ?
Merci de votre aide
Reprend l'extrait du tableau représenté en haut de la page 8. Dans la cellule F3, il faut entrer la formule de la composante de l'accélération sur x fournie dans mes message précédent. En supposant que la valeur numérique de la constante (k/m) est en cellule B1, cela donne :
-B$1*((D3^2+E3^2)^0.5)*D3
Pour la composante de l'accélération suivant y, il faut rentrer en cellule G3 :
-B$1*((D3^2+E3^2)^0.5)*E3-9.81
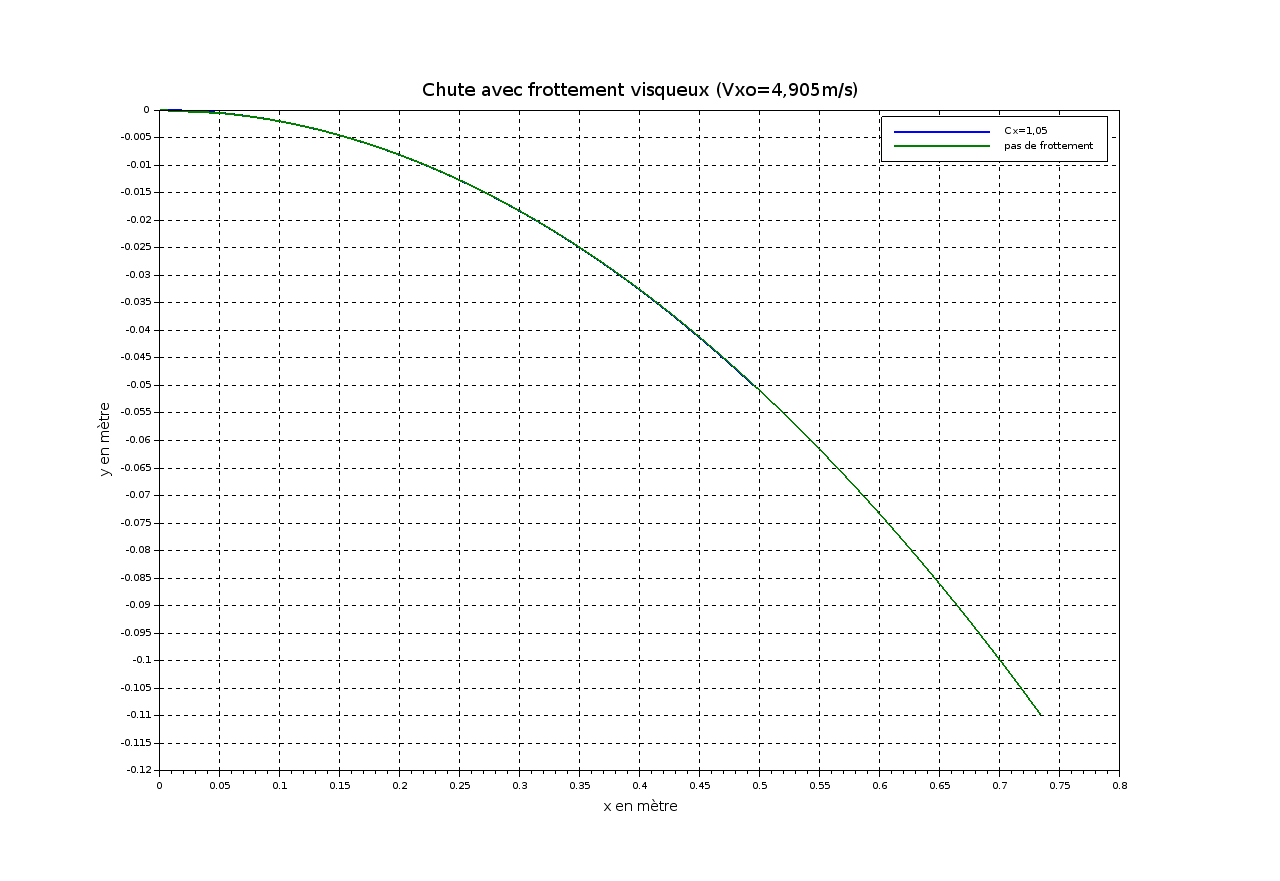
Cela dit, tes valeurs numériques sont vraiment mal choisies (c'est de la faute de ton énoncé peut-être). Sur des parcours aussi courts et des vitesses aussi faibles, la force de frottement reste toujours très faible devant le poids (2,5% du poids environ), l'écart entre la trajectoire théorique en absence de frottement et la trajectoire en présence de frottement est pratiquement indiscernable graphiquement. Pour illustrer mon propos, voici une simulation sous Scilab... Les deux courbes sont pratiquement confondues. Pour observer un écart, il faudrait étudier la chute sur une hauteur plus importante...
PS : j'ai déjà eu l'occasion de dire ce que je pense de l'approximation consistant à assimiler la voiture à un point matériel dans une telle situation. Les deux conditions nécessaire à une approximation correcte ne sont pas du tout remplies ici. Ton professeur aurait mieux fait de te demander d'étudier la trajectoire d'un ballon de football ou d'une balle de golf avec et sans frottement ; là : les écarts sont significatifs et assimiler le ballon ou la balle à un point matériel est correct pour peu que l'on néglige l'influence de la rotation du ballon ou de la balle sur lui-même (elle-même).
je suis maintenant en train d'essayer de recopier le tableau j'ai ainsi repris vous equation sur les axe mais je ne sais pas a quoi correspond la case D1 du tableau je bloque dessus d'ailleurs la valeurs de k/m dans notre enoncer est elle bien de 0.0064 ?
Bonjour !
Si tu projettes sur les deux axes la relation vectorielle traduisant la relation fondamentale de la dynamique :
\overrightarrow{a}=-\frac{k}{m}.\Vert\overrightarrow{v}\Vert.\overrightarrow{v}-\overrightarrow{g}
tu obtiens les deux équations fournies dans mon message du 12-03-19 à 18:50.
J'aimerai savoir comment vous arrivez à obtenir la projection des vecteurs de frottements+poids sur les deux axes. Je bloque sur le passage des grandeurs vectorielles aux grandeurs scalaires
Merci d'avance !
Tu connais sûrement l'expression de la norme d'un vecteur en fonction de ses deux composantes (coordonnées) :
Si tu projettes la relation vectorielle suivant x puis suivant y :
Évidemment :
....
Pour le tableur : la première ligne est à modifier. GMt n'a pas d'intérêt ici mais tu peux entrer la valeur de (k/m) en B1.
La ligne 3 correspond aux valeurs initiales. En D3 il faut entrer la valeur de la vitesse initiale suivant x (en m/s) : 4.9.
Les composantes de l'accélération que le tableur doit calculer en F3 et G3 n'ont pas tout à fait les valeurs que tu as indiquées. Je t'ai fourni les "formules" à utiliser...
j'ai maintenant des composante de l'acceleration en x et y mais je comprend toujours pas comment a partir de ca je suis censé trouver une valeur initial pour passer le ravin il faut faire des iteration apres ?
j'ai ca pour le moment je fait quoi apres ?
ah oui suite au mail de mes prof le coef de trainée est de 0.4 ce qui est bien plus logique
Franchement : j'ai l'impression d'avoir en face de moi des interlocuteurs différents qui posent des questions sans s'être donné la peine de lire attentivement mes messages, au moins tous ceux postés aujourd'hui. Je veux bien corriger l'extrait de tableur fourni mais je penses avoir répondu en détail aux questions d'ordre théorique...
Remplace GMt par k/m en A1 et fait apparaître en B1 la valeur numérique de ce quotient. Avec tes valeurs (ou celles d'un de tes camarades ???), on n'arrive pas à 2.45E-4...
Le pas de calcul que je t'ai conseillé n'est pas non plus la valeur affichée en F1.
La vitesse initiale n'a pas de composante suivant y. Il faut donc entrer "0" en E3 et entrer en D3 la vitesse initiale. Commence par entrer celle correspondant à la vitesse initiale en absence de frottement. Le document fourni explique comment compléter la ligne 4.
Recopie ensuite cette ligne 4 jusqu'à la ligne 100. Tu peux alors tracer la trajectoire d'équation y=f(x) en représentant les variation des valeurs de la colonne C en fonction des valeurs de la colonne B.
Il te resteras alors à ajuster la valeur de Vox (cellule E3) pour que la trajectoire passe par le point désiré.
Franchement : ce travail est infaisable par quelqu'un qui n'a pas un minimum de bases en mécaniques et un minimum d'entraînement à l'utilisation d'un tableur...
Alors (pour moi) tu as bien répondu. J'ai réussi mais seulement avec excel et la manière de faire du pdf que tu as posté mais je ne vois pas comment le faire avec scilab.
Bonjour QuentinButel
Si je comprends bien, vous êtes une promo à travailler sur le même sujet ? Plutôt sympa mais il ne faudrait pas que cela vire à la cacophonie sur le forum. Si tu connais bien le niveau des autres étudiants qui interviennent, tu pourrais peut-être les aider. Je n'arrive pas à déterminer ce qui les bloques.
Concernant l'utilisation de Scilab, je veux bien t'aider mais pas à partir de zéro. Il faut que tu ais un minimum de pratique de ce logiciel. Le mieux serait que tu proposes un début de programme que je pourrais ensuite d'aider à améliorer.
Le plus simple consiste à construire la matrice X dont les quatre colonnes sont :
X(1)=x ; X(2)=y ; X(3)=x'=vx ; X(4)=y'=vy.
Bonjour
J'ai effectué la méthode d'Euler sur Excel qui a bien fonctionné, cependant j'ai tenté d'effectuer de même avec la fonction ODE sur scilab. Cependant j'obtiens un code avec des erreurs que je n'arrive pas à résoudre. Pourriez vous m'aider ? Merci
clear()
//Déclarer les variables et les fonctions nécessaires au calcul :
v0x=5;
v0y=0;
tfinal=10;
//frictions/m
km=-0.0006125/3*10^-4;
//On veut trouver x'(t) et y'(t) grâce à x''(t) et y''(t) grâce à la fonction ode résolution d'une équation différentielle linéaire du 1er ordre.
//********************************************************************************************************
//********************************************************************************************************
// déclaration de la fonction y' en fonction de y et t
function yp=f4(t, y)
// déclaration des conditions initiales et du pas de temps de calcul (t varie de 0 à Pi par pas de 0.1s)
yp0=v0x;
t0=0;
t=0:0.1:%pi;
yp=ode(yp0,t0,t,f2)
endfunction
//********************************************************************************************************
//********************************************************************************************************
// déclaration de la fonction x' en fonction de x et t
function xp=f3(t, x)
xp0=v0x;
t0=0;
t=0:0.1:%pi;
xp=ode(xp0,t0,t,f1);
endfunction
//********************************************************************************************************
//********************************************************************************************************
// déclaration de la fonction x'' en fonction de x' et t
function xpp=f1(t, xp, yp)
xpp=km*((xp^2+ yp^2)^0.5)*xp
endfunction
//********************************************************************************************************
//********************************************************************************************************
// déclaration de la fonction y'' en fonction de y' et t
function ypp=f2(t, yp, xp)
ypp=km*((xp^2+yp^2)^0.5)*yp
endfunction
//********************************************************************************************************
//********************************************************************************************************
// déclaration des conditions initiales et du pas de temps de calcul (t varie de 0 à Pi par pas de 0.1s)
x0=0
t0=0;
t=0:0.1:%pi;
// résolution de l'équation différentielle de f3
x=ode(x0,t0,t,f3);
// déclaration des conditions initiales et du pas de temps de calcul (t varie de 0 à Pi par pas de 0.1s)
y0=0
t0=0;
t=0:0.1:%pi;
// résolution de l'équation différentielle de f4
yp=ode(y0,t0,t,f4);
plot2d(y, x);
a=gca();
a.title.text='Mouvement de la voiture';
a.x_label.text='Position sur x';
a.y_label.text='Position sur y';
Tu résouds tes deux équations différentielles comme si elles étaient indépendantes. Or : elles sont couplées : ax dépend de vx mais aussi de vy ; ay dépend de vy mais aussi de vx. Il faut donc une résolution simultanée du système des deux équations. Le plus simple consiste à construire la matrice X dont les quatre colonnes sont :
X(1)=x ; X(2)=y ; X(3)=x'=vx ; X(4)=y'=vy.
Cela apparaît bien dans l'expression de Xo : valeur de X en t=0.
On définit alors Xprime qui correspond à la dérivée de X par rapport à t : Les quatre colonnes de Xprime vont donc être :
f(1) = X(3) : valeur de vx
f(2)=X(4) : valeur de vy
f(3) : expression de ax en fonction de X(3) et X(4)
f(4) : expression de ay en fonction de g,X(3) et X(4)
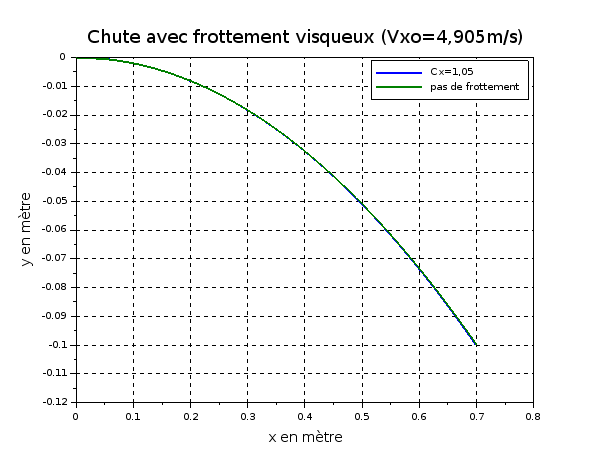
Pour tracer la trajectoire, il faut alors représenter les valeurs de la deuxième colonne de X en fonction des valeurs de la première colonne.
Pour visualiser l'influence des frottement, je rajoute dans le même repère le tracé de la parabole correspondant à l'absence de frottement. On voit clairement qu'à d'aussi faibles vitesses, l'influence des frottements est totalement négligeable. Les deux courbes sont pratiquement confondues.
Mon code Scilab :
clear()
//mouvement de chute avec frottements fluides
g=9.81;
//Valeur de k/m pour Cx=1.05
h=1.0054e-2;
//conditions initiales
xo=0;yo=0;Vox=4.905;Voy=0;
//équation différentielle
function f=Xprime(t,X)
f(1)=X(3)
f(2)=X(4)
f(3)=-h*sqrt(X(3)^2+X(4)^2)*X(3)
f(4)=-h*sqrt(X(3)^2+X(4)^2)*X(4)-g
endfunction
//Valeurs initiales de X et de t
Xo=[xo;yo;Vox;Voy];
to=0;
//intervalle d'étude et nombre de points de calculs
t=linspace(0,0.143,200);
//Résolution du système d'équations différentielles
X=ode(Xo,to,t,Xprime);
//création d'une fenêtre graphique et effacement de son contenu éventuel
scf(1)
clf(1)
//équation de la trajectoire parabolique correspondant aux mêmes conditions initiales en absence de frottement
y=linspace(0,-0.1,200)
x=sqrt(-2.*y.*Vox^2./g);
//Tracés des deux courbes dans la fenêtre 1.
plot(X(1, ,X(2,
,X(2, ,x,y,'thickness',2)
,x,y,'thickness',2)
xgrid()
xlabel('x en mètre','fontsize',3)
ylabel('y en mètre','fontsize',3)
title('Chute avec frottement visqueux (Vxo=4,905m/s)','fontsize',4)
legend('Cx=1,05','pas de frottement')
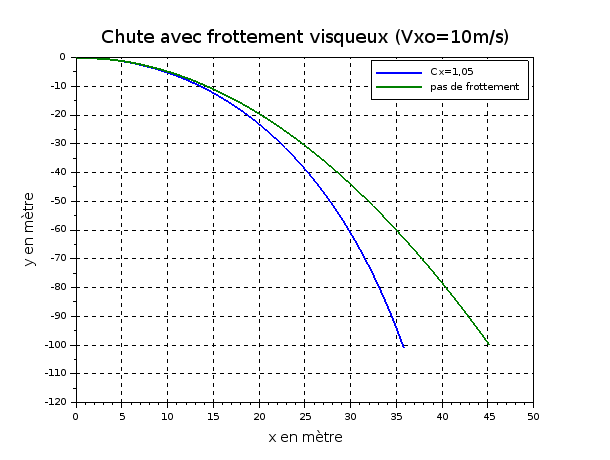
Imagine que le même véhicule saute d'une falaise de 100m de hauteur avec une vitesse initiale horizontale de 10m/s. Les vitesses acquises deviennent beaucoup plus importantes ; la force de frottement n'est plus négligeable devant le poids comme le montre la simulation ci-dessous. Cependant : sur les premiers mètres de chute, l'écart reste très faible.
pour le tracé des courbes, la sélection des colonnes utilisent les mêmes codes que les smileys...
plot(X(1, ,X(2
,X(2 ,x,y,'thickness',2)
,x,y,'thickness',2)
le code est :plot( X(1,x),X(2,x) ,...) ou le "x" doit être remplacé par ":"
Je ne sais pas comment désactiver les smileys...
bonsoirs j'ai essayer votre programme et il y a une erreur a votre fonction plot j'ai fait des recherche et j'ai du mal a trouver la solution malgrès mes nombreux essaie pouvais vous clarifier vos explication qquand a cette fonction
Il y a effectivement une erreur dans l'expression "plot" car je ne sais pas comment dans l'éditeur de texte du forum bloquer l'apparition des smiley. Je pensais pourtant mon rectificatif de 15h08 explicite. Pour plus de clarté, je recopie la ligne avec l'éditeur d'équations pour éviter les smiley ;
il s'agit de représenter les variations des ordonnées (deuxième colonne de X) en fonction des abscisses (première colonne de X) puis de superposer à cette courbe la parabole correspondant à l'absence de frottement d'équation y=f(x). Sinon, le programme tourne très bien sur mon pc. J'utilise l'option 'thickness' pour augmenter l'épaisseur de trait.
Bonjour, je n'arrive pas a comprendre dans le programme pourquoi la courbe n'atteint pas l'axe des abscisses.
Bonjour teum
Puisque ici, y est constamment négatif, l'axe des abscisses est l'axe horizontal au-dessus des courbes. Par hypothèse : l'instant initial correspond à x=0 et y=0 avec Vyo=0 : la trajectoire passe donc par l'origine du repère et admet en ce point l'axe (Ox) comme tangente.
Ensuite : l'énoncé initial (je sais : tout cela commence par durer...) demande que la trajectoire passe par le point de coordonnées (0,7m , -0,1m) ; pour cette raison, j'ai arbitrairement limité la trajectoire aux points tels que y -0,1m.
-0,1m.
J'aurais juste une dernière question. Pour déterminer Cx, je me suis documenté et j'ai vu que la démarche est très compliqué ( pour notre niveau en tout cas). J'ai vu que pour une voiture de tourisme, Cx varie entre 0.3 et 0.4 comme vous l'indiquez dans votre message du 12-03-19 à 18:50 cependant je ne vois pas comment déterminer Cx=1.05 qui est indiqué dans le programme Scilab.
Merci de votre aide
La dynamique des fluides est un des domaines de la physique les plus délicats. Ce n'est pas par hasard que l'on continue toujours à faire des études d'aérodynamisme en soufflerie... Le Cx d'un solide est très délicat à déterminer : il dépend, de la forme du solide, de son état de surface et aussi de la vitesse ! Le considérer fixe comme dans ce problème est une approximation valide que dans un certain domaine de vitesse. Bref : à ton niveau, il faut le considérer comme une valeur expérimentale en général fournie par les énoncés. La valeur 1,05 est invraisemblable pour une voiture.
Comme déjà dit, cette étude est truffée d'invraisemblances : franchement : assimiler une petite voiture à un point matériel avec des distances parcourues à peine supérieures à la longueur de la voiture : c'est vraiment n'importe quoi quand le mouvement de la voiture n'est pas une translation. Si les objectifs de cette étude sont bien de faire réfléchir à l'influence des frottements et d'initier à la programmation, étudier la trajectoire d'un ballon de football ou d'une balle de tennis ou de golf aurait atteint les mêmes objectifs sans introduire toutes ces invraisemblances !


