Inscription / Connexion Nouveau Sujet
Etude d'un circuit en régime sinusoidal
Bonsoir, pourriez vous m'aider pour cet exercice s'il vous plait je n'arrive pas à le faire.
J'ai seulement répondu à la question 1 :
Zeq = 1/ZR + 1/ZC + ZL
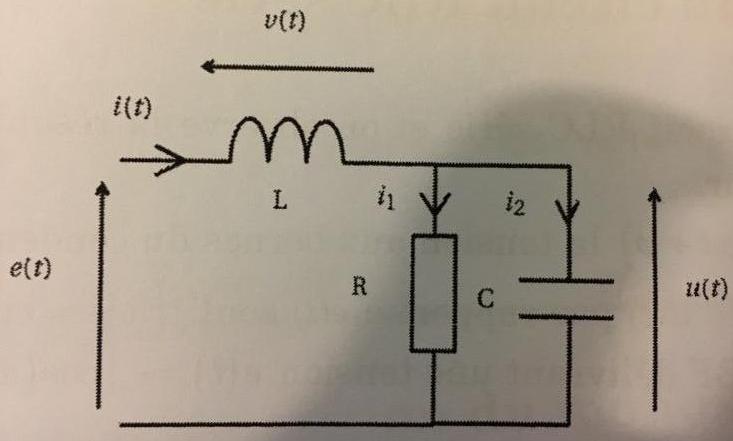
Soit le circuit suivant :
1. Déterminer l'expression de l' impédance équivalente Zeq du circuit.
2. On se place à la pulsation  telle que LC
telle que LC ² = 1 et RC
² = 1 et RC =1 Montrer que L
=1 Montrer que L =R et que l'impédance équivalente Zeq s'écrit Zeq = R(1+j)/2.
=R et que l'impédance équivalente Zeq s'écrit Zeq = R(1+j)/2.
3. A cette pulsation  , montrer que le circuit équivaux à une résistance Req en série avec une bobine d'inductance Leq. Exprimer Req en fonction de R et Leq en fonction de L.
, montrer que le circuit équivaux à une résistance Req en série avec une bobine d'inductance Leq. Exprimer Req en fonction de R et Leq en fonction de L.
4. Déterminer i en fonction de R et e. Sachant que e(t) = emcos( t) , montrer que i(t) =
t) , montrer que i(t) =
 2
2
5. A l'aide de ponts diviseurs de courant, exprimer i1 et i2 en fonction de i. En déduire i1(t) et i2(t) en fonction de em, ,t et R
,t et R
6. A l'aide de ponts diviseurs de tension, exprimer u et v en focntion de e. En déduire u(t) et v(t) en fonction de em,  et t
et t
7. Vérifier qu'on aurait pu retrouver plus facilement v(t) et u(t) connaissant i(t) et i1(t) en appliquant directement des lois de Kirchhoff complexes.
Bonsoir
Ta réponse est fausse : L est en série avec l'association (R//C). Commence par calculer l'impédance équivalente à l'association (R//C) puis ajoute-là à ZL. Tu ne va pas obtenir ton résultat qui est d'ailleurs nécessairement faux : on ne peut pas ajouter une impédance à l'inverse d'une impédance ! Question d'homogénéité !
Tu devrais être capable de rectifier ton expression de l'impédance et d'avancer un peu dans les calculs.
Je te laisse proposer une solution.
Bonsoir et merci de votre réponse.
Notons Zeq1 l'impédance équivalente entre R et C
1/Zeq1 = (1/ZR) + 1/(ZC )
D'où Zeq1 = (ZC ZR)/(ZC+ZR)
On en déduit Zeq = Zeq1 + ZL
Pour la question 2 pour la premiere partie il suffit d 'isoler C et d'obtenir C=1/(R ) et d'injecter cette expression dans LC
) et d'injecter cette expression dans LC ²=1 on obtient donc (L
²=1 on obtient donc (L )/R = 1 soit L
)/R = 1 soit L =R
=R
Plusieurs méthodes plus ou moins équivalentes sont possibles et plus ou moins simple suivant les habitudes prises en cours de math... En voici une :
Pour (R//C) :
Dans ce cas particulier :
Impédance équivalente recherchée :
L'impédance de l'association série de Le et de Re vaut :
Ze=Re+j.Le. ;
;
il suffit d'identifier avec l'expression précédemment obtenue de Ze.
Pour la suite, il faut vraiment que tu étudies ton cours de physique ainsi que ton cours de math.
Tu dois savoir en particulier que, si tu as un quotient de deux complexes (à tout hasard :
,
 ) :
) :
1° : Le module du quotient est le quotient des deux modules ;
2° : L'argument du complexe est la différence des deux arguments.
Je te laisse étudier ton cours et proposer une solution.


