Inscription / Connexion Nouveau Sujet
Etude d'un circuit avec deux condensateurs identiques
Bonjour, voila l'exercice sur lequel je bloque:
On considère le circuit suivant dans lequel les deux condensateurs C1 et C2 ont la même capacité C.
Les condensateurs ne sont pas chargés quand les interrupteurs K1 et K2 sont ouverts.
On donne C = 1,0 µF, L = 5,0 mH, R = 200  et E = 10 V.
et E = 10 V.
Les questions sont les suivantes:
1. A t = 0 , on ferme K1, K2 restant ouvert.
1.1. Quelle relation lie les charges q1 et q2 à tout instant ?
1.2. Déterminer la charge des deux condensateurs au bout d'un temps très long. Faire l'application numérique.
1.3. Quelle est énergie emmagasiné par le système dans ces conditions? Faire l'application numérique.
Pour ces 3 premières questions, j'ai dit que q1 = q2 quelque soit t, car K2 étant ouvert, les deux condensateurs sont en série, et q1(0) = q2(0).
Ensuite, en assimilant les deux condensateurs à un seul de capacité C/2, et les deux résistances à une seule de résistance 2R, j'en déduit l'équation différentielle : donc
, donc
, ce qui donne q(
 ) = 50*10^-7 C.
) = 50*10^-7 C.
Pour l'e=énergie, ui + 2Ri² = Ei, donc Ei = 2Ri² +0.5dEc/dt alors, l'ennergie emmagasiné par le système vaut  Ec = Ec(
Ec = Ec( ) - Ec(0) = (1/4)cE² = 2.5*10^-6 J.
) - Ec(0) = (1/4)cE² = 2.5*10^-6 J.
C'est pour les questions suivantes que je bloque:
2. On suppose que le régime précédant est atteint, on ferme alors K2, K1 restant fermé et on choisit cet instant comme nouvelle origine des temps.
2.1. Quelles seront les charges des deux condensateurs au bout d'un temps très long?
Quelle sera énergie emmagasiné par le circuit dans ces nouvelles conditions?
2.2.En utilisant les lois de Kirchoff, écrire trois équations différentielles faisant intervenir q1, q2, et i.
On pose Q = q1 + q2 et q = q1 - q2
2.3. Établir l'équation différentielle Vérifié par Q.
2.4. Établir l'équation différentielle vérifié par q.
2.5. Exprimer q1(t) et q2(t).
2.6. Déterminer l'expression de i(t).
Je ne demande pas les réponses complètes, mais des pistes pour ne pas rester bloqué, si quelqu'un pourrait m'indiquer une méthode de résolution, ce serait très gentil.
Bonsoir
Pour la partie 2 :
Au bout d'un temps très long, on obtient un régime permanent ; dans ces conditions la tension aux bornes de la bobine (L.di/dt) devient nulle : la bobine se comporte comme un fil de résistance négligeable. L'ensemble {R,C2} est ainsi court-circuité. De plus, en régime permanent aucun courant ne peut circuler dans une branche contenant un condensateur. Avec cela : tu devrais résoudre 2.1
En écrivant les lois de Kirchoff, tu vas obtenir deux équations différentielles couplées c'est à dire faisant intervenir q1, q2 ainsi que leurs dérivées par rapport au temps. Une somme membre à membre puis une soustraction membre à membre permet d'obtenir les équations différentielles vérifiées par Q et q. Tu résous puis revient à q1 et q2...
Je te laisse réfléchir à tout cela et proposer une solution. Cela sera beaucoup plus efficace que de te fournir un corrigé d'entrée...
Quelques remarques concernant la première partie.
OK pour 1.1 ; cela peut se démontrer en remarquant que l'armature gauche du condensateur de droite et l'armature droite du condensateur de gauche sont séparées du reste du circuit par les isolants présents entre les armatures des deux condensateurs :
Pour 1.2 l'étude du régime transitoire n'est pas demandée. Lorsque le régime permanent est atteint :; puisque
.
1.3 : L'énergie accumulée par l'ensemble des deux condensateurs est :
La méthode que tu utilises aurait été très intéressante si l'énoncé demandait un bilan énergétique global. Avec : , il est facile de vérifier que l'énergie totale fournie par le générateur est la somme de celle dissipée par effet Joule et de celle accumulée par les deux condensateurs :
Mais cela n'est pas demandé ici...
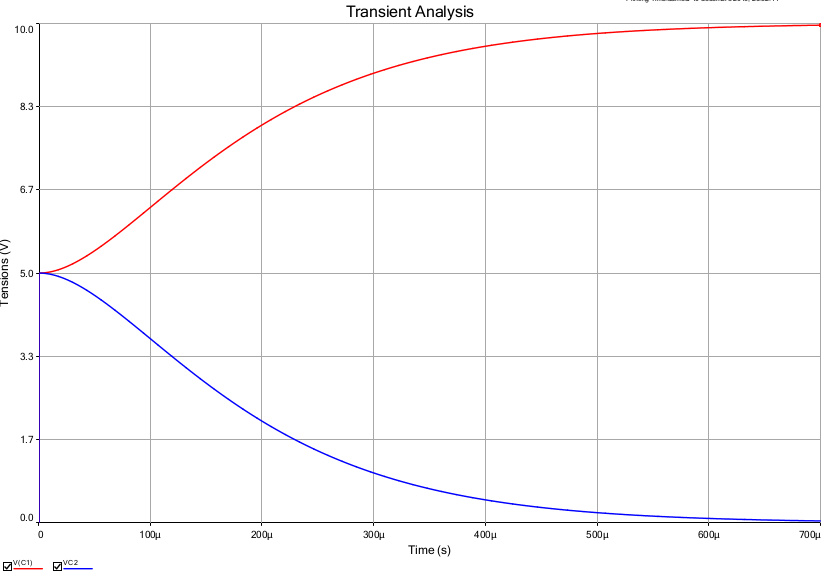
Pour la seconde partie, en complément de mes indications précédentes, voici une simulation représentant les variations de (courbe rouge) et les variations de
(courbe bleue) ; cela devrait t'aider à t'auto-vérifier... Regarde bien ce que valent les coefficients directeurs des tangentes aux deux courbes en t = 0...
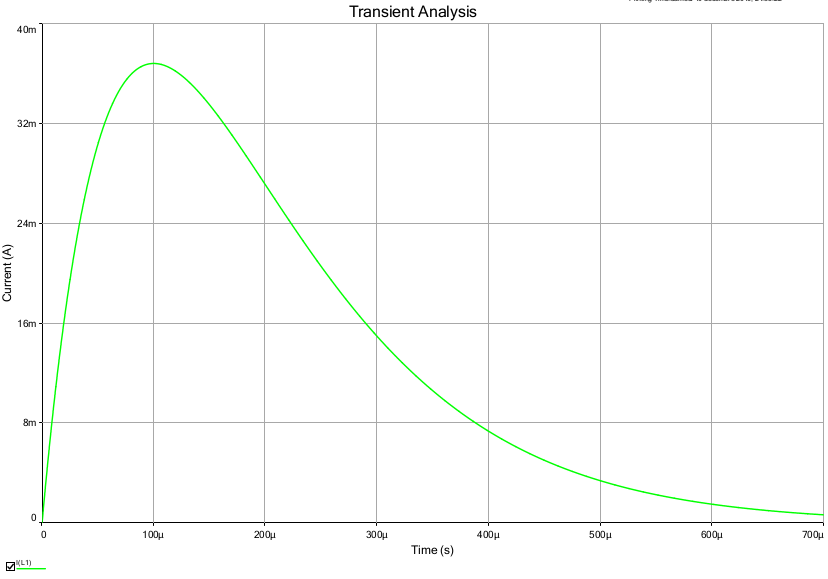
En dessous en vert : la courbe représentant les variations de l'intensité à travers la bobine.
Je te laisse réfléchir et proposer ta solution...
Bonjour, voilà ce que j'ai trouvé:
C2 étant en court circuit avec une résistance, sa charge sera nulle à l' . Les charges se déplaceront vers C1, sa charge sera donc le double de sa charge initiale.
. Les charges se déplaceront vers C1, sa charge sera donc le double de sa charge initiale.
Par la loi des mailles, et
.
On a alors en additionnant: donc
En soustrayant, , donc car i = i2 - i1, on a
donc
.
en forme canonique, ça donne . On forme le polynôme caractéristique, son discriminant est:
, ses racines sont :
.
Donc la solution est de la forme .
X1>0, donc on veut A = 0, et B <0. q(0) = 0, donc B = -EC.
Donc on a:
Donc :
De plus,
Tu as bien travaillé mais tu as commis une erreur ici : . Il faut écrire :
Cette erreur n'impacte pas l'équation différentielle vérifiée par Q mais modifie celle vérifiée par q :
L'équation homogène (second membre nul) peut s'écrire sous la forme :
avec : et
. L'application numérique conduit à :
. Dans ces conditions, l'équation caractéristique a une racine double. Le régime transitoire est qualifié de critique... Je te laisse développer les calculs : la solution générale de l'équation différentielle est de la forme :
Je te laisse déterminer les valeurs des constantes A et B à partir des conditions initiales puis terminer...
Voilà à quoi j'arrive:
q(0) = 0, donc B+CE = 0 donc B = -CE
A t <0, K2 est ouvert, donc i(0-) = 0, et par continuité de l'intensité dans une bobine, i(0-) = i(0+) = 0. dq/dt(0) = A- B donc A = -(RCE)/4L.
B donc A = -(RCE)/4L.
Alors
Donc:
Alors
OK pour les charges. En revanche, tu a commis une étourderie de calcul sur l'expression de i(t). Puisque i(0)=0 et que , la courbe représentative présente nécessairement un extrémum (voir document ci-dessus) ; or ton expression correspond à une exponentielle décroissante.
Remarque : si tu as un peu de temps devant toi (pas certain en math sup !) tu as là l'occasion de réviser les différentes solutions correspondant à une équation différentielle du second ordre :
 <
<  o : choisir par exemple R = 20
o : choisir par exemple R = 20 sans changer les autres valeurs ;
sans changer les autres valeurs ;
 >
>  o : choisir par exemple R = 2,00k
o : choisir par exemple R = 2,00k


