Inscription / Connexion Nouveau Sujet
etude circuit du 2nd ordre
Bonjour, je réalise un exercice sur un circuit du 2nd ordre RLC.
J'ai établi l'équation de uc(t) et donné ses expressions suivant les différents modes (pseudo-périodique, apériodique, critique...) selon les valeurs de R, la résistance. Ensuite, il m'a fallu trouver la valeur de R pour avoir un régime oscillatoire amorti. Jusque là tout allait bien.
Ensuite, je n'ai pas compris la question :
Quelle condition doit vérifier la période T de u(t) pour permettre au régime permanent à 1% près de s'établir dans le circuit pour chaque palier de la tension en créneaux ? Proposez alos une valeur de la frequence f qui verifie cette condition.
C'est-à-dire que signifie que le régime permanent s'établit ? Je ne vois pas où chercher cette condition. Je ne comprends pas la consigne
Merci de votre aide !!
Enoncé complet SVP.
Ce serait étonnant que l'exercice soit donné dans le cadre général (donc en devant examiner tous les régimes (pseudo-périodique, apériodique, critique...)
Il y a probablement des valeurs de R, L et C dans l'énoncé qui permettent de se cantonner dans un des cas.
De plus, on doit probablement deviner que ce circuit est attaqué par un générateur délivrant une tension "carrée" de période T..., mais ce serait mieux que ce soit dit explicitement. (car rien n'impose par exemple que les 2 "alternances" du signal du générateur soient de même durée) ...
Bref, pour pouvoir aider au mieux, il serait bien d'avoir un énoncé complet.

Il faut examiner tous les régimes à une seule question
excusez-moi pour l'imprecision de mon post
Donc voici l'enoncé :
(on a un cicuit RLC)
On a R variable, L= 58 mH et C=150nF
Le GBF fournit un signal carré : 0-6V
1) Etablir l'equation différentielle regissant uc(t) (le condensateur est initialement déchargé)
2)L et C sont fixes, donner les expressions possibles de uc(t) dans les différents modes selon les valeurs de R (c'est là où j'ai fait pour lambda=w0, lambda<wo et lambda>w0)
3) Comment faut-il choisir R pour avoir un régime oscillatoire amorti ? (La j'ai pris R<w0 càd lambda<w0)
4) Quelle condition doit vérifier la période T de u(t) pour permettre au régime permanent (a 1%près) de s'établir dans le circuit pour chaque palier de la tension en créneaux ? Proposez alors une valeur de la fréquence f qui vérifie cette condition.
C'est à cette dernière question que je n'y arrive plus.
Merci de votre aide
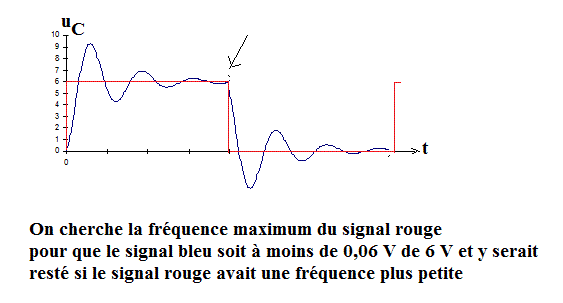
Sur le flanc d'entrée qui passe de 0 à 6 V ...
La tension sur le condensateur finit par valoir 6 volt ... elle y arrive en oscillant ou non suivant les valeurs de L, C et R.
Lorsque, la tension sur le condensateur est dans la plage 6 V +/- 1% de 6 volts --> donc dans la plage [5,64 ; 6,06] Volt et n'en sortira plus (par exemple à cause des oscillations), on dit que la tension du condensateur est et reste à moins de 1% de la tension en régime établi.
Il faut chercher la fréquence maximum du "carré" d'entrée pour que la tension sur le condensateur soit à moins de 0,06 V de la tension qu'il atteindrait pour un fréquence quasi nulle du carré d'entrée.
----
En pseudo périodique, il faut probablement que e^(-(T/2) * 2L/R) = 0,01
avec la fréquence du signal rouge f = 1/T. Vérifie ...
...
Sauf distraction. 
J'ai compris votre explication mais comment arrivez-vous à expliquer qu'on arrive à e^(-(T/2) * 2L/R) = 0,01 ?
Sij'essaie d'isoler T, cela fait :
-(T/2) * 2L/R = ln 0,01
T=R ln (0,01)/L
Cela me donne quelque chose comme -145, n'est-ce pas bizarre ?
De même, je n'ai pas su quoi prendre comme valeur pour R car R est variable. Je savais juste que pour être en régime oscillatoire amorti, on devait avoir R<1 kOhm
Correction d'une distraction, il fallait lire : e^(-(T/2) / (2L/R)) = 0,01 (en pseudo périodique)
e^(-(T/2) / (2L/R)) = 0,01
-(T/2) * R/(2L) = ln(0,01)
(T/2) * R/(2L) = ln(100)
T = 4L/R * ln(100)
T = 18,4 * L/R
f max = 1/18,4 * R/L
f max = 0,054 * R/L
Pas vérifié. 
D'accord, merci !
Cela me donne une fréquence d'environ 1560 Hz, cela semble-t-il correct ?
R est variable, j'ai pris la valeur trouvée à la question 3, cela est-il correct ?
Petit oubli : comment également arrivez-vous à savoir qu'en régime pseudo-périodique, on pose : e^(-(T/2) / (2L/R)) = 0,01
Quelle est l'expression de uc(t) dans le cas "pseudo périodique" en réponse à un echelon de tension de 6 V ?
Elle devrait ressembler à : Uc(t) = 6.e^(-R/(2L).t) * (cos(...) ... )
Et donc l'amplitude de l'oscillation diminue au cours du temps par le "e^(-R/(2L).t))
Cette oscillolation aura une amplitude de 1% de 6 volts après un délais t1 tel que :
e^(-R/(2L).t1)) = 1%
soit donc pour e^(-R/(2L).t1)) = 0,01
Et t1 correspond à la demi période du signal carré. (voir sur le dessin)
--> e^(-R/(2L) * T/2)) = 0,01
Qui conduit à T = 18,4 * L/R
et donc à f = 1/T = 1/(18,4)*R/L = 0,054.L/R
Sauf distraction. 
Sauf distraction. 


