Inscription / Connexion Nouveau Sujet
Equilibre intérieur dans un solide
Bonjour, j'espère que vous aller bien ! Je viens solliciter votre aide par rapport a un exercice de résistance des matériaux qu'on vient de débuter. Merci d'avance !
Voici l'énoncé
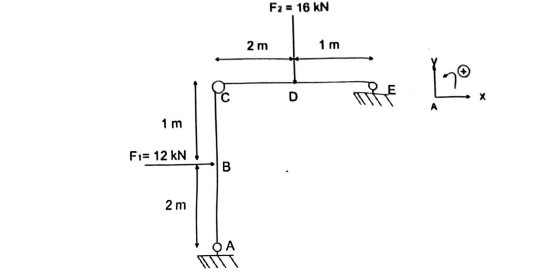
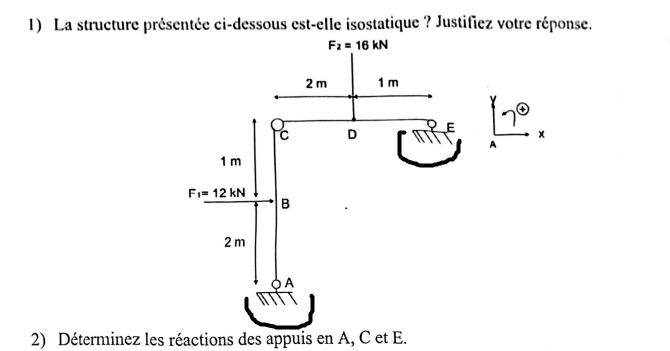
1- La structure est elle isostatique ?
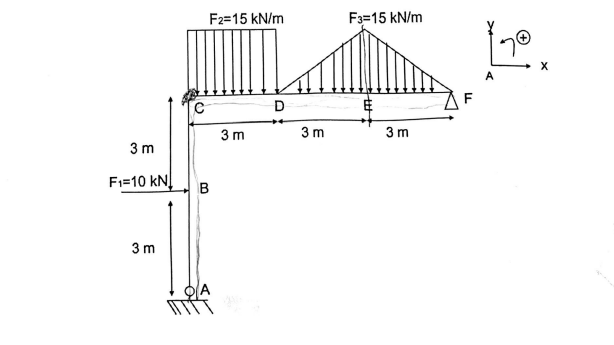
2-Déterminer les réactions d'appuis en A, C et en F.
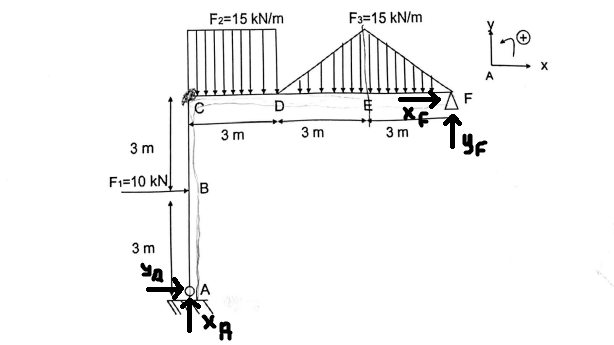
3- Déterminer les réactions d'appuis en A et en F.
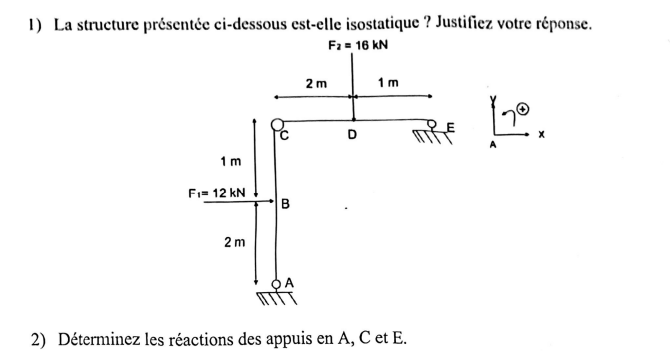
1-Les réactions d'appuis
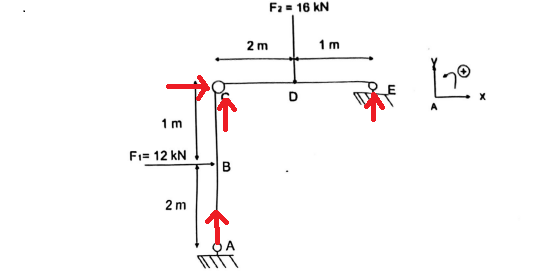
J'ai considéré en C qu'on a une liaison rotule
Ps: Mon soucis avec les types d'appuis c'est que notre prof nous a dit que c'est pas normalisé et j'ai vu des documents qui considéré que telle représentation d'appuis signifie un truc, alors que dans notre cours ou ailleurs c'est le contraire ( je fais référence aux appuis simples et aux articulations)
Bonsoir,
En effet, d'un support à l'autre ce ne sont pas les mêmes représentations, les tiennent s'apparentent à ce schéma :
Tu as donc effectivement :
* une liaison articulation en A et E
* une liaison rotule en C.
Il faut donc que tu reprennes ton schéma par rapport aux efforts de liaison en jeu et que tu appliques le principe fondamental de la statique.

Celle que j'ai envoyé ce était pour montrer que c'est différent avec celui de notre cours.
Celle que j'ai au niveau de l'articulation c'est un appui simple et l'appui simple c'est l'articulation.
Maintenant j'aimerais savoir si peut importe la représentation qu'on choisit en C on a toujours une liaison rotule ? Et doit on séparer le système en deux système pour trouver la valeur des réactions?
Articulation ou rotule tu auras deux efforts en jeu dans un plan, cela ne change donc rien.
Avant de te lancer dans des calculs, l'énoncé te demande quel est le degré d'hyperstatisme de cette structure.

Effectivement du coup je vais devoir choisir une autre interprétation c'est a dire :
En A, C et E on a une articulation
Donc d=2*3( nombre d'articulation)-3*2(nombre de solides)=0
Le système serait donc isostatique, ce qui signifierait qu'il y a autant d'équations que d'inconnues pour résoudre le problème.
Reprends ton schéma avec toutes les inconnues de liaison en A, C et E puis applique le principe fondamental de la statique :
* équation de la résultante statique selon x ;
* équation de la résultante statique selon y ;
* une à deux équations de moment judicieusement choisies selon z.

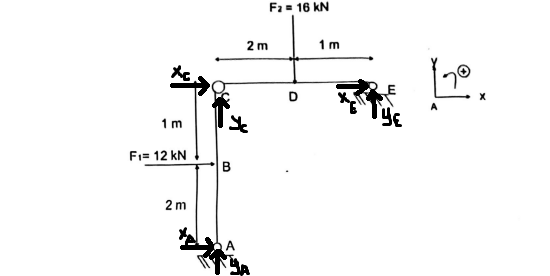
Système AC:
Suivant x: Xc+Xa+F1=0
Suivant y: Yc+Ya=0
Moment suivant z en A: -F1*2-Xc*3=0
 Xc=
Xc=; Xa=
;
Systeme CE:
Suivant x: Xc+Xe=0
Suivant y: Ye+Yc-F2=0
Moment suivant Z en E: -3*Ye+1*F2=0
 Xe=
Xe=; Ye=
; Yc=
; Ya=
As-tu fini par une vérification en injectant les expressions trouvées dans les équations initiales (bonne pratique) ?

C'est que tout semble bon alors  !
!
Pour le deuxième cas, reviens aux représentations des liaisons dans mon message du 25-01-25 à 18:31 (je sais, c'est perturbant mais nous devons faire avec !) :
* en A c'est effectivement une articulation ;
* en revanche en F c'est un appui simple, donc un seul effort en jeu selon y.
Ce qui devrait te ramener à un système isostatique.
Cela m'aurait paru brutal de commencer un cours de RDM avec des systèmes hyperstatiques.

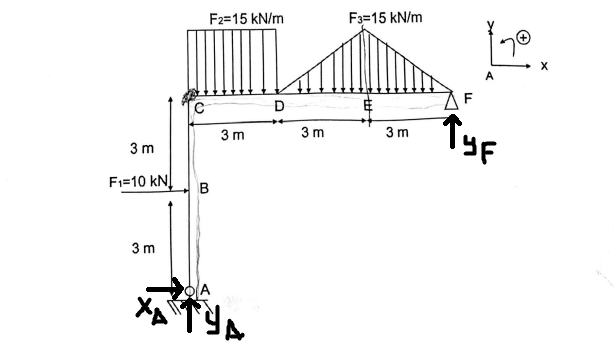
On vérifie l'hyperstaticité:
d=1*1+2*1-3*1=0 La structure est bien hypostatique
On a d'après la condition d'équilibre:
Suivant X: Xa+F1=0
Suivant Y: Yf+Ya-3F2-3*F3=0
Moment suivant Z en A: -3F1-1.5F2-9*F3+9Yf=0
 Xa=-F1; Yf=
Xa=-F1; Yf=; Ya=
J'ai une dernier question sur la détermination du nombre de solides. On compte 1 solide lorsque il est adossé au sol (il y a des hachures ) et quand il y'en a pas on ne compte pas le truc comme un solide ?

On vérifie l'hyperstaticité:
d=1*1+2*1-3*1=0 La structure est bien hypostatique
Isostatique*
Je ne suis pas sûr que comprendre ce que tu entends pas "hachures" : s'agit-t-il de la répartition linéique de l'effort ?
Pour ton étude statique il faut ramener les répartitions linéiques à des efforts équivalents F2 et F3 :
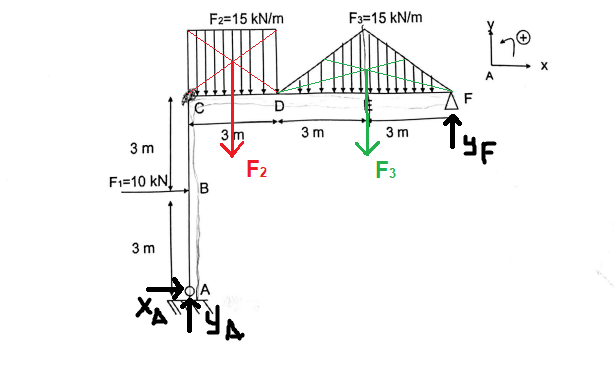
En intégrant l'effort linéique sur la longueur indiquée sur la figure :
* F2 = 15*3 = 45 kN
* F3 = 6 * 15 / 2 = 45 kN (je suppose que le 15 kN est atteint en E car énoncé imprécis)
Tu peux alors appliquer ton PFS pour aboutir aux valeurs des efforts aux liaisons)

En gros je parlais de ça
Sur la première figure on a compter les deux comme solides à cause des hachures ?
Et l'autre structure y a un solide vu que l'autre n'a pas de hachures ?
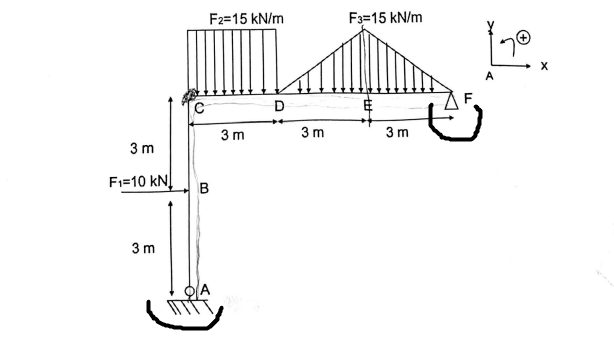
Il s'agit de la représentation d'un socle, puisque la liaisons en jeu est l'articulation (en A).
S'il n'y avait pas eu la représentation de cette dernière, cela aurait été un encastrement.
Concernant l'appui simple en F, oui, les hachures auraient également pu être représentées en-dessous.

Tu comptes le nombre de poutres dans la structure (ici 2 dans chaque cas) et après tu regardes les liaisons en jeu pour établir les degrés de liberté (et donc les efforts en jeu dans un modèle plan).

En fait tu as plusieurs méthodes pour déterminer le degré d'hyperstatisme : pour la 2ème structure, tu peux "casser" fictivement les encastrements pour faire émerger plusieurs solides => ici j'en compte donc 2 :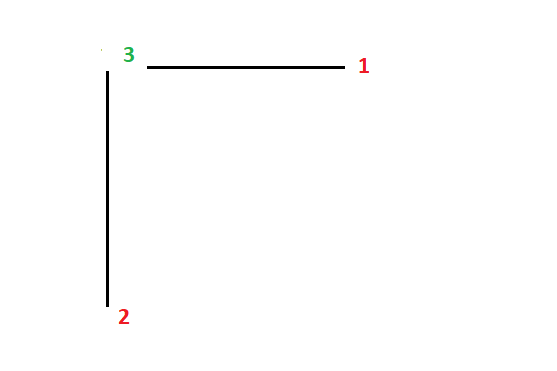
On peut alors déterminer le degré d'hyperstaticité total.
On est dans un problème plan, donc pour chaque solide, on peut écrire 3 équations :
* résultante par rapport à x,
* celle par rapport à y,
* et équation de moment en un point par rapport à z.
Il y a donc 3 x 2 = 6 équations à écrire pour ces deux solides.
Concernant les liaisons en jeu :
* un encastrement apporte 3 inconnues statiques ;
* une articulation 2 inconnues ;
* un appui simple 1 inconnue.
On a donc ici : 3 + 2 + 1 = 6 inconnues
D'où finalement un degré d'hyperstaticité total Htot = nombre d'inconnues - nombres d'équations = 6 - 6 = 0.
Généralisable à des structures bien plus complexes.
En fait tu as plusieurs méthodes pour déterminer le degré d'hyperstatisme : pour la 2ème structure, tu peux "casser" fictivement les encastrements pour faire émerger plusieurs solides => ici j'en compte donc 2 :

On peut alors déterminer le degré d'hyperstaticité total.
On est dans un problème plan, donc pour chaque solide, on peut écrire 3 équations :
* résultante par rapport à x,
* celle par rapport à y,
* et équation de moment en un point par rapport à z.
Il y a donc 3 x 2 = 6 équations à écrire pour ces deux solides.
Concernant les liaisons en jeu :
* un encastrement apporte 3 inconnues statiques ;
* une articulation 2 inconnues ;
* un appui simple 1 inconnue.
On a donc ici : 3 + 2 + 1 = 6 inconnues
D'où finalement un degré d'hyperstaticité total Htot = nombre d'inconnues - nombres d'équations = 6 - 6 = 0.
Généralisable à des structures bien plus complexes.

Ma méthode est plus pour appréhender la structure et le degré d'hyperstatisme.
As-tu déjà essayé d'isoler le système dans son ensemble et d'établir le système de trois équations statiques classiques ?
Pour cela, tu peux t'appuyer sur mon schéma du 26-01-25 à 20:15
En effet je n'avais pas vu : attention à bien expliciter les bras de levier dans ton équation de moment, tel que j'ai fait avec mon schéma.
As-tu remplacer les valeurs de F1, F2 et F3 et fait la vérification usuelle à la fin ?

Oui jai remplacer F1, F2 et F3 (sauf erreur d'inattention je crois que j'ai utilisé votre démarche)
Vérification usuelle ?
Question : En C on a un encastrement, alors pourquoi ça ne figure pas dans les équations ? Yc, Xc et Mzc
Si tu étudiais les deux sous-systèmes, tu sais que cela conduirait à traiter un système de 6 équations à 6 inconnues => pourquoi s'embêter avec alors que tu as moyen de déterminer les efforts aux appuis en isolant le système dans son ensemble ?
Ce faisant, tu verras prochainement dans ton cours de RDM que cette coupure fictive sera utile pour expliciter le torseur de cohésion et tracer les diagrammes des efforts.
En gros, pour tracer les diagrammes des efforts pour une poutre soumise à un effort concentré et/ou à un champ linéique, on imagine qu'une section droite S de centre de gravité G et d'abscisse x (repère défini) établit une coupure fictive en x de la poutre :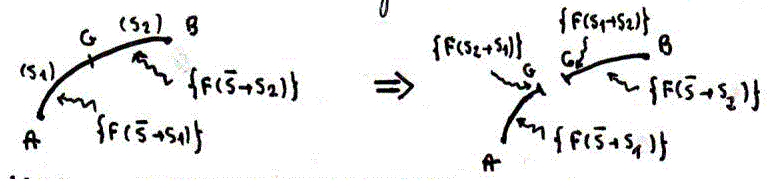
Par définition, le torseur de cohésion (ou torseur des efforts intérieurs) s'écrit :
Si tu appliques le principe fondamental de la statique, on démontre que ce torseur des efforts intérieurs peut s'écrire en un torseur des efforts extérieurs appliqués à la section ou
, au signe près :
("+" ce qui est à droite)
("-" ce qui est à gauche)
Voilà pourquoi tu pourras analyser une poutre à gauche ou à droite de la section droite d'abscisse x (au signe près) pour tracer des diagrammes d'efforts intérieurs ou encore pour calculer ce torseur.