Inscription / Connexion Nouveau Sujet
Equilibre hydrostatique
Bonsoir,
J'ai un petit problème à propos de l'équation de l'hydrostatique :
Où P est la pression et la force volumique.
Dans le cas d'une distribution sphérique, où ,
alors (où
est la masse volumique qui dépend du rayon r),
et ,
donc :
Pourtant si je raisonne sur une petite portion de la sphère (de volume r²sin( )drd
)drd d
d ), alors :
), alors :
Il s'exerce (le poids)
et les forces de pressions sur les côtés s'annulent, et il reste la force s'exerçant en r :
et celle s'exerçant en r+dr :
Donc, à l'équilibre, la somme de ces forces étant nulle, on trouve :
Donc après simplification par :
Donc :
ce qui est contradictoire avec
Auriez-vous une explication ? Merci.
Bonjour,
Je ne comprends pas pourquoi le poids est radial chez vous ? J'ai raté quelque chose ?
Avec un petit schéma, je crois que cela serait plus clair...
D'autre part, on fait plutôt un développement en puissances de dans l'expression
et on ne garde que je premier ordre.
Un poids radial vous choque ? On est attiré vers le centre de la Terre non ? 
De toute façon l'expression du poids importe peu.
Et pour l'histoire du premier ordre, je ne suis pas tellement convaincu :/
Et si vous commenciez par donner un énoncé complet ? Avec un schéma ? En disant quel est le système étudié ?
Toussa quoi....
Pour "l'histoire du premier ordre", tant pis pour vous, je ne suis pas un gourou de secte, je ne cherche pas à vous convaincre, je ne suis pas dans la croyance en ce qui concerne la physique, et encore moins les calculs.
L'énoncé est le suivant :
Soit un astre fluide à symétrie sphérique où P(r) est la pression,  (r) la masse volumique et r la distance au centre de l'astre.
(r) la masse volumique et r la distance au centre de l'astre.
Le champ de pesanteur dû à l'astre est noté .
En utilisant l'équilibre de l'astre, déterminer une relation entre g(r) et  (r).
(r).
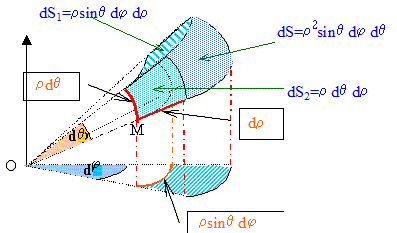
Le système que j'étudie est la petite portion de sphère de volume r²sin( )drd
)drd d
d
(dans le schéma il faut lire r au lieu de  ).
).
Et pour moi, si l'on considère la fonction f:r r²P(r), alors :
r²P(r), alors :
(r+dr)²P(r+dr)-r²P(r)=f(r+dr)-f(r)=( f/
f/ r)dr
r)dr
Il s'agit bien là d'un premier ordre, non ?