Inscription / Connexion Nouveau Sujet
Équilibre d’une barre de traction
Bonsoir, je bloque totalement sur cette question :
Un peu de contexte avant :
On place une barre de 1.2kg dans une chambranle de porte de largeur D=70cm. Expliquer qualitativement comment cette barre peut tenir en équilibre sans fixation. Faire un schéma avec toutes les forces.
Ça pas de soucis j'ai supposé que la barre (équipée d'un ressort de raideur k calculé dans la question précédente) ne glissait pas car il existait une force de frottement entre les deux solides qui s'oppose au déplacement de la barre qui l'empêche le glissement des deux solides.
Cependant, on me demande de calculer le coefficient de frottement statique a sachant que si la longueur au repos l0 est inférieure à 70.2 cm la barre tombe
C'est là où je n'arrive pas...
Une première idée était de faire :
Bilan des forces à l'équilibre :
0= mg + Force rappel élastique + R
En projetant sur Ox:
N=k(leq-l0)
En projetant sur Oy:
T=mg
Ainsi a=T/N
Or en remplaçant on connaît l0 mais pas l, c'est pour ça que je ne suis pas du tout sûr... Merci d'avance
(Je mets mon schéma quand même)
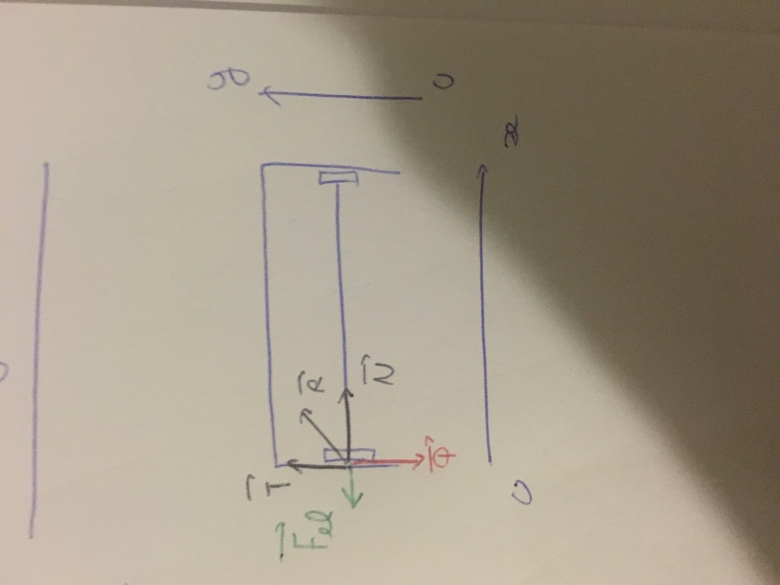
** image supprimée **
Hello
Tu connais la largeur du chambranle: D = 70 cm 
Et attention, le chambranle a 2 côtés et la barre 2 extrémités 
donc on aurait 70.2-70= leq-l0 ?
Oui normalement il devrait avoir les forces des deux côtés mais je ne voulais pas l'alourdir pour que ça reste lisible pour le forum..
Cependant, le fait qu'il y ait ça en double, est ce que mon coefficient n'est plus valable ?
J'ai pas très bien compris 
En gros on a T= 1/2mg car il est présent à gauche et à droite ?
Et N vaut toujours k(leq-l) car il est seulement présent à gauche ? (Vu qu'il y a qu'un ressort) ?
Donc on aurait a = mg/2k(leq-l0) où leq-l0= (70.2-70).10^-2 ?
Bon alors ... on va essayer de clarifier
quand tu écris "Bilan des forces à l'équilibre" ... quel est le système que tu étudies et dont tu veut le bilan des forces? La barre? Sans doute puisque tu fais intervenir son poids.
Les forces appliquées à la barre sont donc
1/
2/ et
avec
3/ Enfin et
avec
Et
Tu projettes sur Oy et tu obtiens la condition souhaitée sur 
D'accord, donc on aurait en projetant sur Oy
T (g) =mg
Donc T(g)u N(g)
Soit mg 1/2 * delta l * u
Mais que représente le delta l dans l'expression de N(g) ?
Hello
Ton système est la barre (qui contient le ressort). Ce sont donc les forces et
qui nous intéressent, valant (3eme loi de Newton):
Système à l'équilibre:
Donc (cf ce qui était posé hier soir)
(en intensité bien sûr)
La condition de non mouvement est:
(même chose à droite)
Donc
Soit
Avec biens sûr
La longueur au repos l0 limite peut donc s'écrire, pour un coefficient de frottement statique donné:
C'est bien une fonction décroissante de  ("si la longueur au repos l0 est inférieure à 70.2 cm la barre tombe")
("si la longueur au repos l0 est inférieure à 70.2 cm la barre tombe")
Et, cette valeur limite étant trouvée "expérimentalement", elle permet de calculer  pour ce chambranle
pour ce chambranle
C'est plus clair ainsi ? 
D'accord !!! C'est direct plus clair quand on pose bien les choses, je m'entraînerai à le refaire. Merci beaucoup en tour cas 

 En prépa au moins autant qu'ailleurs, il faut répéter et répéter les exercices tant que les étapes du raisonnement ne sont pas fluides
En prépa au moins autant qu'ailleurs, il faut répéter et répéter les exercices tant que les étapes du raisonnement ne sont pas fluides
