Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths supForum Supérieur de maths sup PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths sup
Partager :

Equations différentielles

Posté par
fenchyr 13-08-15 à 09:24

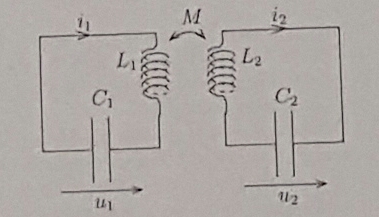
Bonjour, je suis bloquer dans l'établissement des equations différentielles vérifiées par u1 (t) et u2 (t) dans le circuit suivant.
On nous donne L1C1=L2C2=1/(wo2)
=M/(L1L2)
=(L1L2)

J'ai obtenu deux expressions analogues tels que :

d2u1(t)/dt + (wo)2u1(t) = -M(wo2)di2(t)/dt

Mais on nous demande de faire apparaître et dans ces equations et même en essayant de jouer avec le relations je ne trouve rien de concret.

Pourriez vous m'aider s'il vous plaît ?  

Merci d'avance

Posté par
fenchyrre : Equations différentielles 13-08-15 à 09:27

Désoler j'ai oublier le circuit

Equations différentielles

Posté par
vanoisere : Equations différentielles 13-08-15 à 11:13

Citation :
d2u1(t)/dt + (wo)2u1(t) = -M(wo2)di2(t)/dt

di2/dt peut s'exprimer en fonction d'une dérivée de u2 par rapport au temps.

Tu dois trouver deux équations couplées que tu peux transformer en un système de deux équations différentielles à variables séparées en effectuant une "somme membres à membres" et une "différence membres à membres". Tu pourras poser, par exemple, : y = u2 + u1 et x = u2 - u1.
Bon courage !

Posté par
fenchyrre : Equations différentielles 13-08-15 à 11:40

D'accord je voit merci, juste une petite précision s'il vous plaît, dans la question suivante on pose u1=Aexp(jwt) (en notation complexe) et de même pour u2 avec B qui remplace A. On nous demande quelles sont les valeurs possibles de w ?

Instinctivement j'aurai dit toutes les valeurs de 0 à + mais la fin de la question nous demande d'étudier les relations entre A et B pour chaquese valeurs de w, je ne sais plus quoi faire ....

Posté par
vanoisere : Equations différentielles 13-08-15 à 12:42

Citation :
Instinctivement j'aurai dit toutes les valeurs de 0 à +

Je ne crois pas !
Remplace dans tes deux équations différentielles u1 et u2 par leurs expressions complexes proposées. Tu vas constater que w vérifie une certaine équation dont tu vas devoir trouver les solutions...

Posté par
fenchyrre : Equations différentielles 13-08-15 à 14:24

Je trouve w= wo ou w=-wo ou
W=wo/(1+) ou w=-wo/(1+) je viens aussi de remarque que j'ai mal recopier l'énoncé, =(L1/L2)...

Posté par
fenchyrre : Equations différentielles 13-08-15 à 17:14

Une dernière chose s'il vous plaît, on rajoute une résistance R dans chaque circuit et on pose L=L1=L2 et C=C1=C2
On nous demande de résoudre les equations en u1 et u2 ( en posant h=L/R et en supposant hwo 》1) puis de les interpréter en fonction des liens obtenus entre A et B.

J'obtient en posant s=u1+u2 et a=u1-u2,u1=(s+a)/2

Soit u1 = exp (t/(2h(1+)) *(Kcos(wo/(1+))+Dsin(wo/(1+))) + ( la même chose en remplaçant les 1+ par 1-) /2

Et la n'ayant pas de condition iniriales je ne pense pas pouvoir aller plus loinos au niveau des réponses mais je ne voit pas comment trouver le lien  

Posté par
vanoisere : Equations différentielles 13-08-15 à 18:39

Citation :
Je trouve w= wo ou w=-wo ou
W=wo/(1+) ou w=-wo/(1+) je viens aussi de remarque que j'ai mal recopier l'énoncé, =(L1/L2)...

Je n'ai pas eu le temps de faire le calcul complet mais ton résultat m'étonne : en général, le couplage de deux oscillateurs de même pulsation propre wo conduit à deux pulsations propres différentes, une de valeur supérieure à wo, l'autre de valeur inférieure à wo.
En règle générale, les fréquences et les pulsations sont toujours comptées positives. Cela ne restreint pas la généralité du problème physique si on pose : u = A.cos(wt)+B.sin(wt) ou u = D.cos(wt+).

Posté par
vanoisere : Equations différentielles 13-08-15 à 18:57

Citation :
Je trouve w= wo ou w=-wo ou
W=wo/(1+) ou w=-wo/(1+) je viens aussi de remarque que j'ai mal recopier l'énoncé, =(L1/L2)...

Je n'ai pas eu le temps de faire le calcul complet mais ton résultat m'étonne : en général, le couplage de deux oscillateurs de même pulsation propre wo conduit à deux pulsations propres différentes, une de valeur supérieure à wo, l'autre de valeur inférieure à wo.
En règle générale, les fréquences et les pulsations sont toujours comptées positives. Cela ne restreint pas la généralité du problème physique si on pose : u = A.cos(wt)+B.sin(wt) ou u = D.cos(wt+).

Posté par
fenchyrre : Equations différentielles 13-08-15 à 19:03

JE voit ce que vous voulez dire mais si je ne distingue pas le cas w=wo il y a un passage ou je ne peut diviser par wo-w...

Posté par
vanoisere : Equations différentielles 13-08-15 à 19:27

Voici le calcul des fréquences propres. On peut faire un peu plus simple que la méthode proposée par l'énoncé et mon message précédent.
équations différentielles (les deux points désignent la dérivée seconde par rapport au temps):
\overset{..}{u_{1}}$+$\omega_{0}^{2}u_{1}=-MC_{2}\omega_{0}^{2}\overset{..}{u_{2}}=-\frac{M}{L_{2}}\overset{..}{u_{2}}
\overset{..}{u_{2}}+\omega_{0}^{2}u_{2}=-MC_{1}\omega_{0}^{2}\overset{..}{u_{1}}=-\frac{M}{L_{1}}\overset{..}{u_{1}}
En régime sinusoïdal établi, dériver deux fois par rapport au temps est équivalent à multiplier par (-w2) ; d'où le système :
\left(-\omega^{2}+\omega_{0}^{2}\right)u_{1}=\frac{M}{L_{2}}\omega^{2}u_{2}
\left(-\omega^{2}+\omega_{0}^{2}\right)u_{2}=\frac{M}{L_{1}}\omega^{2}u_{1}
Des solutions sinusoïdales d'amplitudes non nulles pour u1 et u2 imposent :
\left(-\omega^{2}+\omega_{0}^{2}\right)^{2}=\frac{M^{2}}{L_{2}L_{1}}\omega^{4}=\alpha^{2}\omega^{4}
D'où les deux cas :
\left(-\omega^{2}+\omega_{0}^{2}\right)=\alpha\omega^{2}
\left(-\omega^{2}+\omega_{0}^{2}\right)=-\alpha\omega^{2}
Je te laisse continuer, sachant que physiquement : -1 < <1.

Posté par
vanoisere : Equations différentielles 13-08-15 à 20:08

Citation :
Soit u1 = exp (t/(2h(1+)) *(Kcos(wo/(1+))+Dsin(wo/(1+))) + ( la même chose en remplaçant les 1+ par 1-) /2

Et la n'ayant pas de condition iniriales je ne pense pas pouvoir aller plus loinos au niveau des réponses mais je ne voit pas comment trouver le lien  

En utilisant la méthode que je viens d'exposer et en cherchant des solution de la forme A.exp(rt) on remarque que r peut prendre les valeurs :
r1=jw1-1/(2h(1-)) et r2=jw2-1/(2h(1-)) où w1 et w2 désigne les pulsations propres calculées précédemment.
On obtient donc les solutions sinusoïdales précédente multipliées par un terme d'amortissement exponentiel : exp(-t/2h(1-)). Attention au signe ! La solution que tu proposes correspond à une amplitude qui croît exponentiellement vers l'infini : impossible !
Pour les conditions initiales, si rien n'est dit dans l'énoncé, il faut imaginer un des condensateur chargé, l'autre déchargé, et l'absence de courant initial :
à t = 0 :
u_{1}=U_{0}\qquad u_{2}=0\qquad\overset{.}{u_{1}}=0\qquad\overset{.}{u_{2}}=0
Le calcul rigoureux est assez laborieux !

Posté par
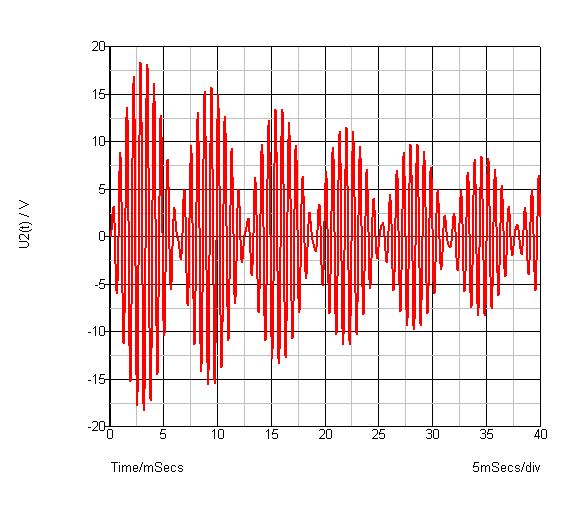
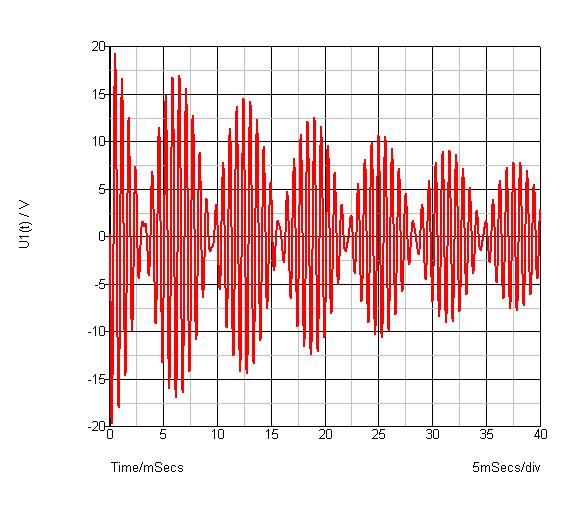
vanoisere : Equations différentielles 13-08-15 à 20:58

Voici une simulation des tensions u2 et u1 en régime transitoire avec :
L=100mH ; C = 100nF ; R = 5 ; =0,1.
J'ai choisi une valeur de très faible de façon que les deux fréquences propres soient très proches. Dans ces conditions, on obtient un phénomène de battement classique, comme on pourrait en obtenir dans de nombreux autres domaines de la physique. On peut remarquer l'amortissement due à la présence des résistances.

Equations différentielles

Equations différentielles

Posté par
fenchyrre : Equations différentielles 13-08-15 à 21:48

Votre résultat avec les r m'arrangerait bien mais je dot utiliser s et a et dzns leurs expressions les sinus ne portent pas de j permettant de retrouver vos r1 et r2....

Posté par
vanoisere : Equations différentielles 13-08-15 à 23:03

Équations différentielles tenant compte des résistances :
\overset{..}{u_{1}}+RC\omega_{0}^{2}\overset{.}{u_{1}}+\omega_{0}^{2}u_{1}=-\frac{M}{L}\overset{..}{u_{2}}=\overset{..}{u_{1}}+\frac{1}{h}\overset{.}{u_{1}}+\omega_{0}^{2}u_{1}
\overset{..}{u_{2}}+\frac{1}{h}\overset{.}{u_{2}}+\omega_{0}^{2}u_{2}$=-$\frac{M}{L}$$\overset{..}{u_{1}}
On cherche des solutions de la forme u1=A.exp(r.t) et u2=B.exp(r.t) ; les deux équations précédentes deviennent:
\left(r^{2}+\frac{r}{h}+\omega_{0}^{2}\right)u_{1}=-\frac{M}{L}r^{2}u_{2}
\left(r^{2}+\frac{r}{h}+\omega_{0}^{2}\right)u_{2}=-\frac{M}{L}r^{2}u_{1}
u1 et u2 devant être des valeurs différentes de zéro, il faut :
\left(r^{2}+\frac{r}{h}+\omega_{0}^{2}\right)^{2}=\frac{M^{2}}{L^{2}}r^{4}=\alpha^{2}r^{4}
On doit envisager deux cas :
\[ \\ \left(r^{2}+\frac{r}{h}+\omega_{0}^{2}\right)=\alpha r^{2}\qquad et\qquad\left(r^{2}+\frac{r}{h}+\omega_{0}^{2}\right)=-\alpha r^{2} \\ \]
En négligeant (1/h)2 devant wo2 comme demandé, on obtient bien les solutions indiquées dans le message précédent. La partie réelle de la solution correspond au terme d'amortissement exponentielles. Les parties imaginaires correspondent aux termes en cosinus...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !