Inscription / Connexion Nouveau Sujet
Equation différentielle RLC
Bonjour à tous,
Dans cet exercice on me demande d'établir l'équation différentielle à laquelle obéit Ur(t).
Cependant, nous avons toujours établi des équations en Uc, en UL , en i ou en q mais jamais en Ur.
C'est pour cela que j'aimerais que l'on m'aide sur ce problème.
Voici le schéma du montage :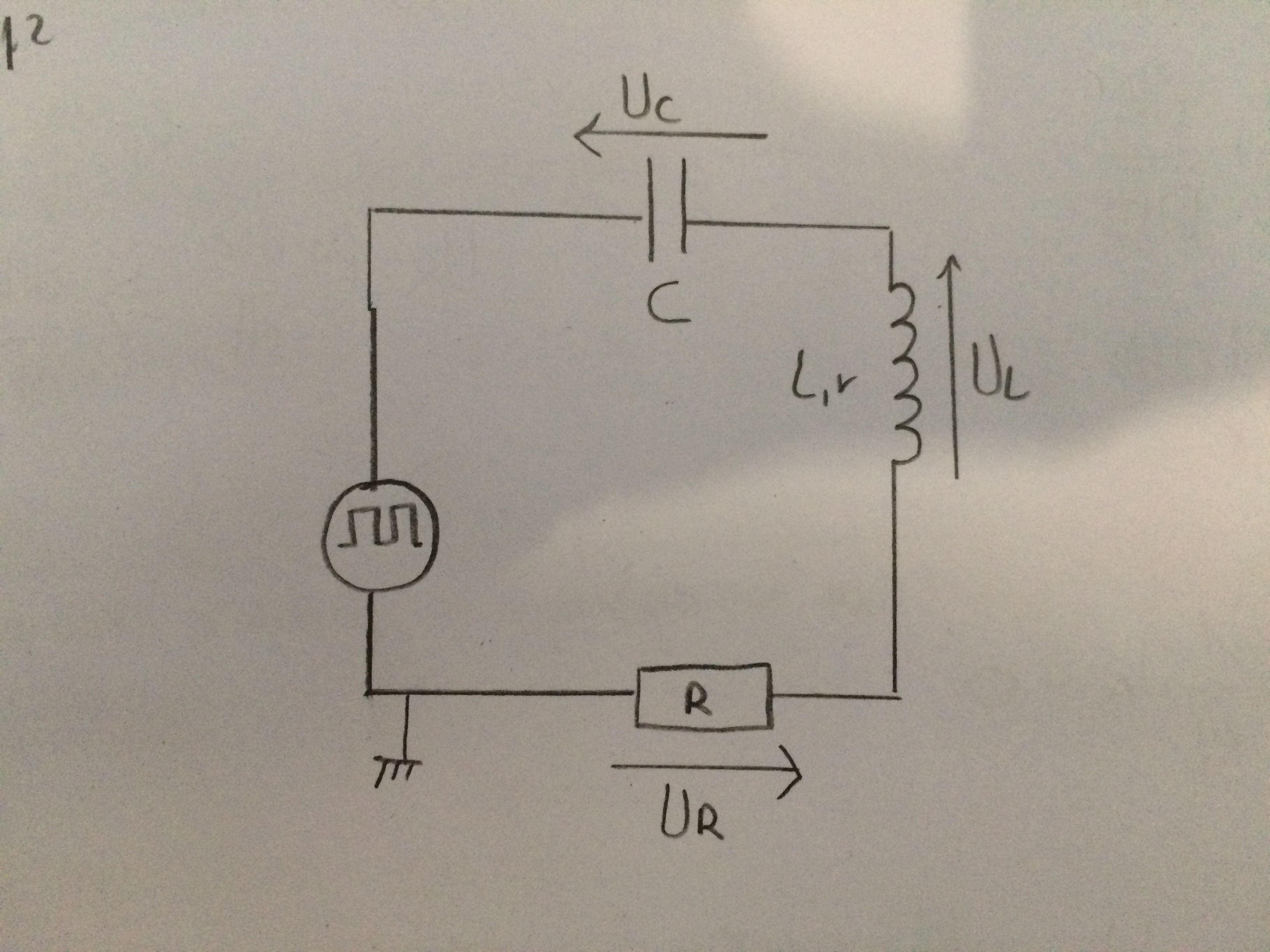
Merci
Menfin ...
Si tu es capable d'établir l'équation i(t) = ... (c'est toi qui l'a dit)
Alors comme, il est évident (voir schéma) que UR(t) = R.i(t) , c'est la loi d'Ohm. ...

Je suis bien d'accord, mais il faut que je présente la solution sous la forme :
( d²Ur / d²t ) + 2 (dUr/dt)+
(dUr/dt)+ 0²Ur = 0
0²Ur = 0
Avec la loi des mailles on a E - Ur - Uc - UL = 0
Mais comment faire pour arriver à ce que je dois obtenir ?
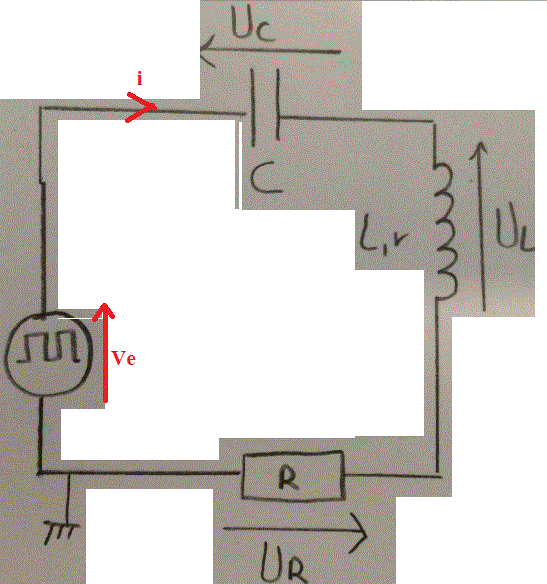
Ve = U(R) + U(C) + U(L)
dVe/dt = dU(R)/dt + dU(C)/dt + dU(L)/dt
Avec :
U(R) = R.i
i = C.dUc/dt
U(L) = L.di/dt
dVe/dt = R.di/dt + i/C + L.d²i/dt²
Or i = U(R)/R -->
dVe/dt = R/R.dU(R)/dt + u(R)/(RC) + L/R.d²UR/dt²
dVe/dt = dU(R)/dt + u(R)/(RC) + L/R.d²U(R)/dt²
d²U(R)/dt² + (R/L).dU(R)/dt + u(R)/(L.C) = (R/L).dVe/dt
Sauf distraction (rien vérifié).



