Inscription / Connexion Nouveau Sujet
équation différentielle guide circulaire en mécanique
Bonjour
Je rencontre un problème à une exercice de mécanique du solide. Je n'arrive pas a répondre aux questions 2 et 3. Je remercia d'avance toutes personnes qui arrivera a répondre a ces 2 question.
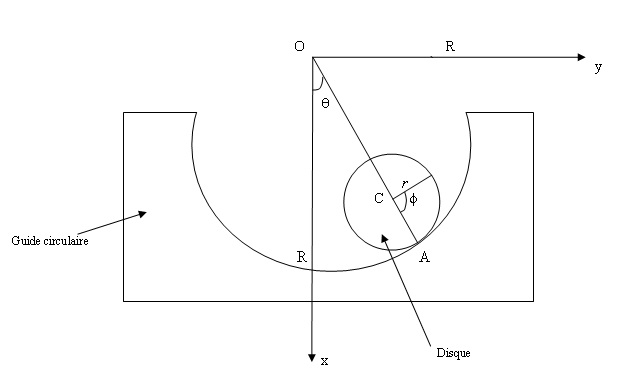
Un disque homogène, de masse m, de rayon r et de centre de masse C, roule sur une guide circulaire. On utilise les angles  et ϕ pour caractériser sa position dans le plan vertical xOy du référentiel R(Oxyz), l'axe Ox étant vertical descendant. On note Icz le moment d'inertie du disque par rapport a son axe de révolution et R le rayon de courbure du guide.
et ϕ pour caractériser sa position dans le plan vertical xOy du référentiel R(Oxyz), l'axe Ox étant vertical descendant. On note Icz le moment d'inertie du disque par rapport a son axe de révolution et R le rayon de courbure du guide.
1) Etablir le lien entre les vitesses angulaire θ ̇ et ϕ ̇ qui découle de la condition de roulement sans glissement du disque sur son guide. Dans toute la suite, on considèrera que cette condition est vérifiée.
J'ai trouver que:
Pas de glissement donc Vg=0
A1 appartient au disque, A2 appartient au guide coincident avec A à l'instant considérer.
VA1=VA2 or VA2=0 car le guide est fixe donc VA1=0
A1 et C appartiennent au disque donc RFC:
VA1=Vc+ disque
disque  CA
CA
R'( r
r z) repère cylindrique mobile
z) repère cylindrique mobile
VA1=Vc+(θ ̇ + ϕ ̇)ez rer
rer
VA1=Vc+r(θ ̇ + ϕ ̇)e
Vc=V0+ θ ̇ez  OC=(R-r)θ ̇ e
OC=(R-r)θ ̇ e
alors VA1=[(R-r)θ ̇ + r(θ ̇ + ϕ ̇)]e
VA1=Rθ ̇+rϕ ̇
2) Justifier très brièvement la conservation de l'énergie mécanique et utiliser cette conservation pour trouver l'équation différentielle du mouvement en  suivante, cette relation étant établie en prenant l'origine de l'énergie potentielle pour la position correspondant θ=π/2:
suivante, cette relation étant établie en prenant l'origine de l'énergie potentielle pour la position correspondant θ=π/2:
1/2 (R-r)^2 θ ̇^2 (m+(ICz /r²))-mg(R-r)cosθ=constante
ICI JE N'ARRIVE PAS A REPONDRE A CETTE QUESTION
3)En déduire la période des oscillations de petites amplitudes
On obtient: To=2
 (R-r)(m+(ICz /r²))/mg)
(R-r)(m+(ICz /r²))/mg)
4)Retrouver l'équation différentielle établie à la question 2 à l'aide du théorème du moment cinétique appliqué au point de contact A entre le disque et le guide circulaire.
ICI JE N'ARRIVE PAS A REPONDRE A CETTE QUESTION
Bonjour
Je rencontre un problème à une exercice de mécanique du solide. Je n'arrive pas a répondre aux questions 2 et 3. Je remercia d'avance toutes personnes qui arrivera a répondre a ces 2 question.
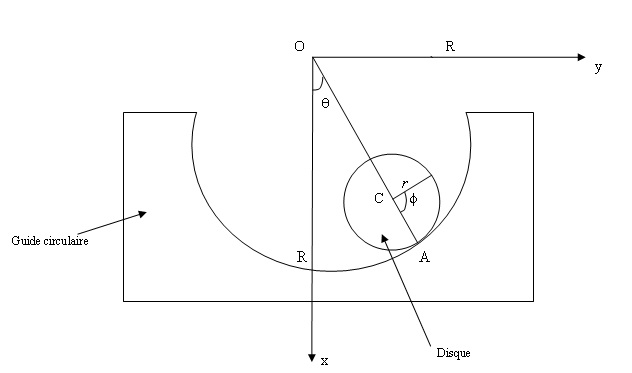
Un disque homogène, de masse m, de rayon r et de centre de masse C, roule sur une guide circulaire. On utilise les angles et ϕ pour caractériser sa position dans le plan vertical xOy du référentiel R(Oxyz), l'axe Ox étant vertical descendant. On note Icz le moment d'inertie du disque par rapport a son axe de révolution et R le rayon de courbure du guide.
1) Etablir le lien entre les vitesses angulaire θ ̇ et ϕ ̇ qui découle de la condition de roulement sans glissement du disque sur son guide. Dans toute la suite, on considèrera que cette condition est vérifiée.
J'ai trouver que:
Pas de glissement donc Vg=0
A1 appartient au disque, A2 appartient au guide coincident avec A à l'instant considérer.
VA1=VA2 or VA2=0 car le guide est fixe donc VA1=0
A1 et C appartiennent au disque donc RFC:
VA1=Vc+disque CA
R'(rz) repère cylindrique mobile
VA1=Vc+(θ ̇ + ϕ ̇)ezrer
VA1=Vc+r(θ ̇ + ϕ ̇)e
Vc=V0+ θ ̇ez OC=(R-r)θ ̇ e
alors VA1=[(R-r)θ ̇ + r(θ ̇ + ϕ ̇)]e
VA1=Rθ ̇+rϕ ̇
2) Justifier très brièvement la conservation de l'énergie mécanique et utiliser cette conservation pour trouver l'équation différentielle du mouvement en suivante, cette relation étant établie en prenant l'origine de l'énergie potentielle pour la position correspondant θ=π/2:
1/2 (R-r)^2 θ ̇^2 (m+(ICz /r²))-mg(R-r)cosθ=constante
ICI JE N'ARRIVE PAS A REPONDRE A CETTE QUESTION
3)En déduire la période des oscillations de petites amplitudes
On obtient: To=2(R-r)(m+(ICz /r²))/mg)
4)Retrouver l'équation différentielle établie à la question 2 à l'aide du théorème du moment cinétique appliqué au point de contact A entre le disque et le guide circulaire.
ICI JE N'ARRIVE PAS A REPONDRE A CETTE QUESTION