Niveau licence

équation différentielle d'un pendule élastique

Posté par
handa 25-11-18 à 21:21

Salut
merci de m'aider
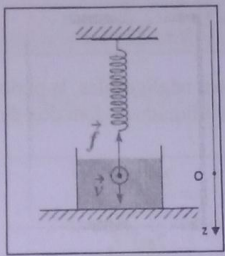
une sphère  de rayon r et de masse m est suspendu à un ressort de raideur k et de longeur à vide $l_{0}$ . lorsqu'elle est en mouvement dans un liquide de coefficient de viscosité $\eta$ , la sphère est soumise à une force de foutrement   $\vec{f}=-6\pi \eta r\vec{v}$   ou v est la vitesse de la sphère.
le point O est confondu avec le centre de gravité de la sphère à l'équilibre, le mouvement de la sphère est pseudo-périodique.
merci de m'aider à déterminer l'équation différentielle.

voila ce que j'ai fait:
à l'équilibre :     $\vec{P}+\vec{F}+\vec{T}=\vec{0} donc : P-F-T=0 \\ donc m.g - \rho .V.g-k.\Delta l_{0}=0$
mais la masse volumique  n'est pas dans les données ?
au cours du mouvement  : $\vec{P}+\vec{F}+\vec{f}+\vec{T}=m.\vec{a}$
comment faire pour déterminer cette équation différentielle en fonction des donnés de l'exercice ( comment faire pour simplifier la masse volumique )

merci d'avance

$équation différentielle d\'un pendule élastique$

Posté par re : équation différentielle d'un pendule élastique 25-11-18 à 21:36

Bonsoir
Pour l'étude dynamique, tu as tout intérêt à prendre l'origine des cotes confondue avec la position d'équilibre de la boule. Ainsi, au cours du mouvement, l'allongement du ressort est (l_o+z)
Sachant que k.l_o est fournie par la relation d'équilibre, l'équation différentielle se simplifie fortement pour donner :

$m\cdot\frac{d^{2}z}{dt^{2}}+6\pi.\eta.r\cdot\frac{dz}{dt}+k.z=0$
La poussée d'Archimède disparaît compte tenu de l'expression de k.l_o.

Posté par re : équation différentielle d'un pendule élastique 25-11-18 à 21:44

oui j'ai compris que l'allongement au cours du mouvement est $\Delta z_{0}+z$
mais pourquoi la poussée d'Archiméde disparaît ?

Posté par re : équation différentielle d'un pendule élastique 25-11-18 à 21:52

Est ce qu'on peut négliger le poids devant les autres forces à l'équilibre ?

Posté par re : équation différentielle d'un pendule élastique 25-11-18 à 21:52

Si tu projettes la RFD que tu as écrite en vecteur sur l'axe, cela donne :

$m\cdot\frac{d^{2}z}{dt^{2}}=m.g-\rho.V.g-6\pi.\eta.r\cdot\frac{dz}{dt}-k.\left(\Delta l_{0}+z\right)$

Or, la relation d'équilibre peut s'écrire :

$k.\Delta l_{0}=m.g-\rho.V.g$

Je te laisse continuer...

Posté par re : équation différentielle d'un pendule élastique 26-11-18 à 00:57

donc l'équation différentielle est :
$\ddot{z}+\frac{6.\pi .\eta .r}{m}.\dot{z}+\frac{k}{m}=0$
merci beaucoup
comment on détermine l'expression de la pseudo-période T en fonction de k,m, $\pi$ , $\eta$ et r. et aussi l'expression de $\eta$ en fonction de m,T et T₀ .

merci d'avance

Posté par re : équation différentielle d'un pendule élastique 26-11-18 à 11:44

Étourderie sans doute : tu as oublié un "z" dans ton équation différentielle :

$\ddot{z}+\frac{6.\pi .\eta .r}{m}\cdot \dot{z}+\frac{k}{m}\cdot z=0$
Pour la résolution de l'équation différentielle, tu peux l'écrire sous la forme :

$\ddot{z}+2\lambda.\dot{z}+\omega_{0}^{2}.z=0$
Tu peux t'inspirer du document ci-dessous en posant K=0. L'étude du régime pseudo-périodique y est détaillée.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

équation différentielle d'un pendule élastique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique