Inscription / Connexion Nouveau Sujet
Equation différentielle Circuit
Bonsoir je ne comprends pas comment trouver les conditions initiales pour trouver la constante K dde mon équation différentielle
U(t)=Ke^(-at)+b/a
dans le schéma ci dessous, on me dit que comme c'est un régime permanant continu
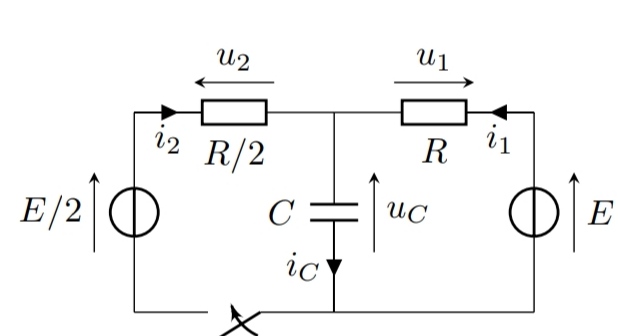
daprès la loi des noeuds, i1+i2=iC
donc i1+0=0 donc i1=0
puis on utilise la loi des mailles et on trouve que U=E etc
mais je ne comprends pas pourquoi i1 vaut O ?
comment trouver les conditions initiales ?
Merci d'avance
Bonjour
Très probablement : l'instant initial correspond à la fermeture de l'interrupteur lorsque le régime permanent est établi dans la maille de droite. Cela correspond à i1=0 et Uc=E.
Daccord mais pourquoi est ce que i1 vaut O ?
Il nya donc plus de courant dans la maille de droite avant t=O ?
pourtant on a encore U=E
L'interrupteur étant ouvert, un courant de charge non nul (i1>0) a existé lorsque le générateur de fém E a été relié au condensateur et à la résistance R (fermeture de la maille de droite) . Ce courant a existé le temps que le condensateur se charge puis ce courant est devenu d'intensité nulle une fois la charge du condensateur terminée : alors Uc=E.
Puisqu'on attend que cette charge soit achevée pour fermer l'interrupteur, l'instant de fermeture de l'interrupteur (t=0) correspond bien à Uc=E et i1=0.


