Inscription / Connexion Nouveau Sujet
Equation differentielle
Bonjour,
Je voudrais reviser pour un DS de physique et je suis bloqué sur un exercice:
Un tube faisant un angle α avec la verticale, tourne autour d'un axe vertical à la vertical à la vitesse ω constante. Sans ce tue, peut se déplacer sans frottement une bille de masse m. Celle ci est accrochée à un ressort de raideur k et de longueur à vide Lo dont l'autre extremité est fixée sur l'axe de rotation ( point O).
1) Dans quel referenciel doit-n se placer pour faire l'étude du mouvement de la bille dans le tube.
J'ai mis le referenciel du tube non galileen
2) Bilan des forces : poids, reaction du support, forces d'inertie et de coriolis.
3)Montrer que le systeme est conservatif
Je n'y arrive pas 
4) Equation differentielle en z
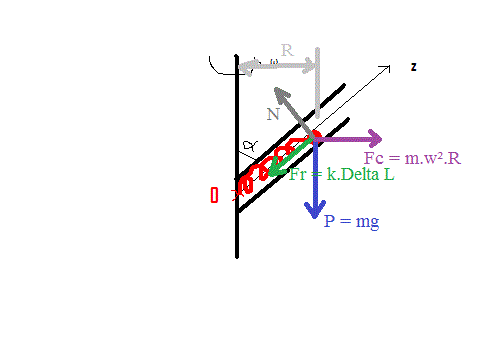
Dans un référentel lié au tube tournant :
La bille est soumise à 4 forces :
son poids : P = mg (vertical vers le bas)
La force centrifuge : Horizontale vers l'extérieur : Fc = m.w².R
La force de rappel du ressort dans la direction du ressort (et donc aussi du tube) : Fr = k.Delta L (avec Delta L l'allongement du ressort).
La réaction du support (tube) : N qui normale au tube puisqu'il n'y a pas de frottement.
-----
Avec z la longueur du ressort : z = Lo + Delta L
R = z.sin(alpha) = (Lo + Delta L).sin(alpha)
Fc = m.w².(Lo + Delta L).sin(alpha)
Résultante des forces suivant Oz : (projection des forces sur Oz) : -Fr + Fc.sin(alpha) - P.cos(alpha)
-Fr + Fc.sin(alpha) - P.cos(alpha) = m.d²z/dt²
- k.(z - Lo) + mw².z.sin(alpha) - mg.cos(alpha) = m.d²z/dt²
m.d²z/dt² + (k - mw².sin(alpha)).z = k.Lo - mg.cos(alpha)
d²z/dt² + (k/m - w².sin(alpha)).z = (k/m).Lo - g.cos(alpha)
-----
A vérifier. 



