Inscription / Connexion Nouveau Sujet
Equation de trajectoire
Bonjour tous le monde j'aurai besoin de votre aide. 
Un archer amateur (Monsieur A) décide de répéter l'expérience de Guillaume Tell , a savoir tirer une flèche dans une pomme placée sur la tête de son fils.
1. En premier lieu, monsieur A pense a tirer horizontalement a une hauteur de 1.10, son fils ayant une taille de 1.05 m et le diamètre de la pomme étant de 10 cm. On appellera vo la vitesse initiale de la flèche. Doutant de la sagesse de cette approche Monsieur A apprend a calculer la trajectoire éventuelle de la flèche .En particulier il trouve la position finale de la flèche sur un parcours de 10m, en négligeant les frottement a l'air et
en prenant vo =80m/s. Pourquoi Monsieur A décide de changer de position ?
Ce que j'ai fait :
ax = 0 avec vo(x) = vocos(
) 
ay = -g vo(y) = vosin()
vx = vocos()
vy = -gt + vosin() = -gt
x(t) =vocos()t = -vot
y(t) = (-1/2)gt^2 + 1,10
Ainsi pour une distance d = 10m on a a 10m: t1 = -d/90 ( problème un temps négatif ? )
y(t1)
1,02
Donc Monsieur A change de stratégie car il lui manque tous de même 8cm pour atteindre la pomme.
2.Poursuivant l'analyse des trajectoires possibles, monsieur A decide de corriger le tir et de lancer la fleche avec un petit angle par rapport au sol . Quel doit etre cet angle afin de placer la fleche en pleine pomme ? (c'est a dire au centre de la pomme (y = 1,10 ).
Ce que j'ai fait:
j'ai poser y(t) = 1,10 car la fleche doit etre a 1,10 a une distance x(t) = d
y(t) = 1,10 (-1/2)gt^2 +vosin()t = 0
car avec un angle 
on a :
y(t) = (-1/2)gt^2 + vosin()t + 1,10
On trouve deux solution t2 = 0 ce qui est logique vus que l'archer tien la flèche a une hauteur de 1,10 et t3 = (160sin())/g
Ainsi x(t3) = 10 m ( on veut qu'il touche le centre de la pomme sur la tete de l'enfant situé a 10m)
x(t3) =vocos()t3
cossin = g/1280
sin2 = 2g/(1280)
0,4379
3. Montrer q'un deuxieme angle de tir possible est ((/2) - ) , mais que cette option sera probablement ecarté par Monsieur A (pour quelles raisons ) ?
je fais y(t4) et je ttrouve y(t4) = -O,73 avec t4 =d/(vocos(90 - 0,4379) puis a partir de la je comprend plus.
4.Expliciter la relation entre la vitesse final de la fleche ( au niveau de la pomme ) et sa vitesse initial
javascript:void(0)
Merci d'avance.
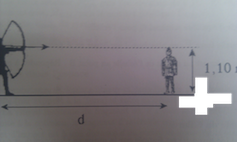
En considérant le plan vertical contenant la trajectoire de la flèche et en prenant pour axes de repère Ox horizontal et Oy vertical dirigé vers le haut, le point O étant la main qui tend l'arc, tandis que vox et voy désignent les composantes horizontale et verticale de la vitesse initiale vo de la flèche, les équations du mouvement de celle-ci sont :
y(t) = - 1/2 gt² + voy t et x(t) = vox t.
D'où y = - 1/2 g (x/vox)² + (voy/vox)x.
Pour un tir horizontal, voy = 0. Je trouve alors, avec les données de l'énoncé, y = - 7,65 cm.
Pour être honnête je comprend pas trop ce que vous avez fait , il vous manquerai pas des constantes telles que 1.10 car la flèche est a y = 1.10
ce que vous avez fait est entièrement la même chose que moi si vous avez lu ce que j'ai écrit je trouve qu' a la distance d la flèche sera a hauteur de 1,02m c'est a dire qu'il lui manque environs 8cm tous comme ce que vous avez écrit ( y = -7,65cm)
bonjour ,
pour la question 4 il suffit de voir que :
sin(2\phi) = 2cos(\phi)sin(\phi)
or les relations de trigo donne:
2cos(\phi)sin(\phi)=2cos(pi/2-\phi)sin(pi/2-\phi)
(en fait on a juste inversé la valeur du cos avec celle du sin et inversement .)
Mais cela donne un angle trop grand pour être réalisé ...
pour la question 5 on demande de trouver une relation entre la vitesse initial et final , or la vitesse sur l'axe Ox ne change pas mais celle sur l'axe Oy varie du fait de la gravitation ... de la tu peux trouver facilement une relation qui te permet de dire:
V_{finale} ~ V_{0}, \phi, g. cad que la vitesse finale dépend de la vitesse initial, de l'angle de départ et de la gravitation.
Voila bonne chance pour la LP112 :p
Re,
oui je retombe sur les même valeurs que toi pour la question 2 ( petit conseille ne remplace pas par les valeurs numériques avant la fin, cad attend d'avoir par exemple sin(\phi) = , pour remplacer par les valeurs numériques du problème)
pour la question 1 moi je dis simplement que la fleche perd de l'altitude car elle est soumis a la force de gravitation, il me semble inutile de calculer la hauteur qu'elle perd a partir du moment ou tu a bien mit en évidence le raisonnement logique.
voila . Si ta d'autre question pour le DM pierre.durand@etu.umpc.fr
Annuler
connectez vous