Inscription / Connexion Nouveau Sujet
Equation d'une trajectoire
Bonjour,
Je ne comprend pas la solution d'un exercice de cinématique du point (math SUP ), pour cela je me tourne à vous afin de m'expliquer .
Voilà comment se présente l'exercice : Un mobile suit une trajectoire sinusoidale de slalom entre des cheminées alignées selon l'axe (Ox). Elles sont espacées d'une distance L=200m.
1) Le véhicule conserve une vitesse constante v0 selon (Ox) et met tt=12s pour revenir sur l'axe après la sixième cheminée. En déduire la vitesse v0. ( Facile)
2)Déterminer l'amplitude la sinusoide pour que l'accélération reste inférieur à 10g en valeur absolue, avec g=9.8m.s-1.
La première question est facile. La deuxième de même. Seulement je ne comprend pas deux points.
1) L'équation de la trajectoire est supposée s'écrire y=asin() . Puisque entre deux maximums de la trajectoire il y'a une distance de 2L.
Mais dans la solution ils ont écrit y=asin().
2) On trouve après calculs que : y=asin() , on calcule l'accélération on trouve
=-a(
)2sin(
). Pour connaitre l'amplitude, on fait norme de l'accélération inférieur ou égale à 10g, mais on à la valeur absolue de sin(..) est inférieur ou égale à 1, en mutlipliant par la valeur absolue de a(
)2 , on trouve que la norme de l'accélération est inférieur ou égale à a(
)2, mais dans la solution ils ont posé directement que a(
)2
 10g
10g
J'espère que vous puissiez m'aider.
Merci d'avance !
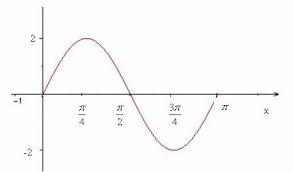
PS : Je ne peux fournir l'image de la trajectoire puisque je l'ai dans un livre, mais je vais fournir un document équivalent . Les cheminées se trouvent respectivement en points :  /4 , 3
/4 , 3 /4 ( On voit bien que la distance entre deux maximums est 2L )
/4 ( On voit bien que la distance entre deux maximums est 2L )
Bonjour
À priori d'accord avec toi pour l'équation de la trajectoire mais erreur sur l'expression de l'accélération. Il n'y a pas de t devant le sinus.
Merci de m'avoir confirmé la faute , j'étais presque devenu fou ^^'
Pour le deuxième point, on a la vitesse selon l'axe (Ox) constante , donc x=v0t+x0 et à t=0 on a x=0 donc x0=0 d'où x=v0t en remplaçant dans l'expression de la trajectoire , on trouve y=asin(( v0t)/L) non ?
v0t)/L) non ?
Non non ^^, on peut remplacer a de l'amplitude par  , on trouvera que
, on trouvera que . Je pense que j'ai trouvé la réponse , pour que la norme de l'accélération soit inférieur ou égale à 10g pour tout t ( le temps ) , il faut que


