Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau autre
Partager :

Equation d'une accélération

Posté par
Hal 07-09-16 à 22:52

Bonjour,

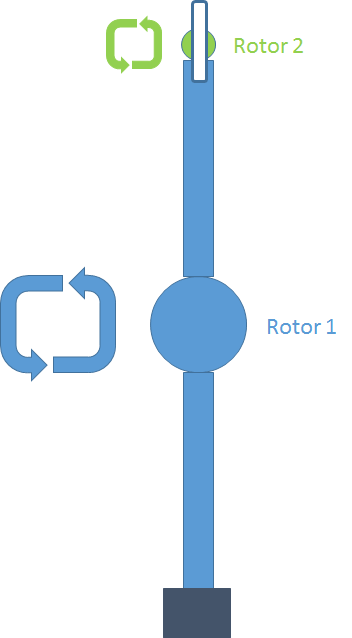
Le schéma ci-joint montre une centrifugeuse avec a l'une de ces extrémité, un second rotor sur lequel est fixé par le milieu un tube contenant un liquide avec des particules.  Les deux rotors tournent horizontalement.

Je souhaite caluler l'accélération subit par une particule M lorsque les deux rotors sont en rotation constante.

Voici ce que j'ai trouvé:

Du point de vue  de la particule, la force centrifuge génénée par le rotor 2 pointe toujours dans la meme direction tandis que celle générée par le rotor 1 décrit un cercle.

Partant de cette constation, j'ai derivé l'équation suivante,


A(t)= \sqrt{(\left\{(\omega1) ^2 \cdot (r1) \right\}\cdot \cos ((\omega 1)t+\theta )+(\omega 2)^2\cdot r2)^2+(\left\{(\omega1) ^2 \cdot (r1) \right\}\cdot \sin ((\omega 1)t+\theta ))^2}

Avec,

(\omega 1) = vitesse angulaire rotor 1
(\omega 2)= vitesse angulaire rotor 2
(r1)= distance a l'axe de rotation rotor 1
(r2)= distance a l'axe de rotation rotor 2
\theta = valeur de l'angle entre les vecteurs A1 et A2 a t=0


Accélération résultante de la somme vectorielle de l'accélération induite par le rotor 1 et de l'accélération induite par le rotor 2. La direction de l'accélération induite par le rotor 2 étant fixe par rapport a la deuxieme qui décrit un mouvement circulaire uniforme.

(J'ai négligé l'action de la pesanteur)


Est-ce correct ?


Merci par avance,

Hal

Equation d\'une accélération

Posté par
vanoisere : Equation d'une accélération 08-09-16 à 12:08

Bonjour
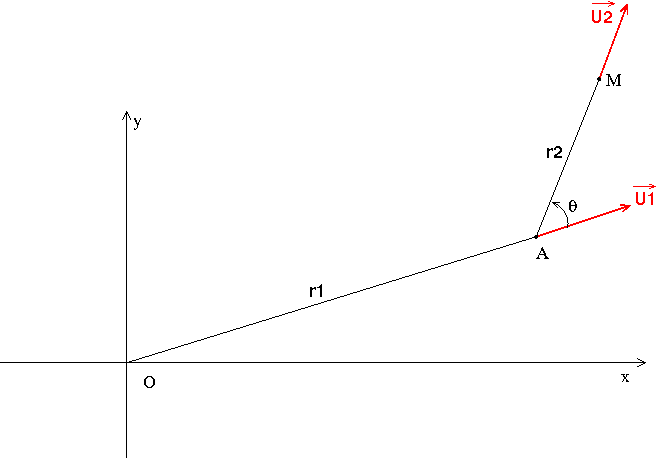
Ai-je bien compris le problème tel que tu cherches à le modéliser ?
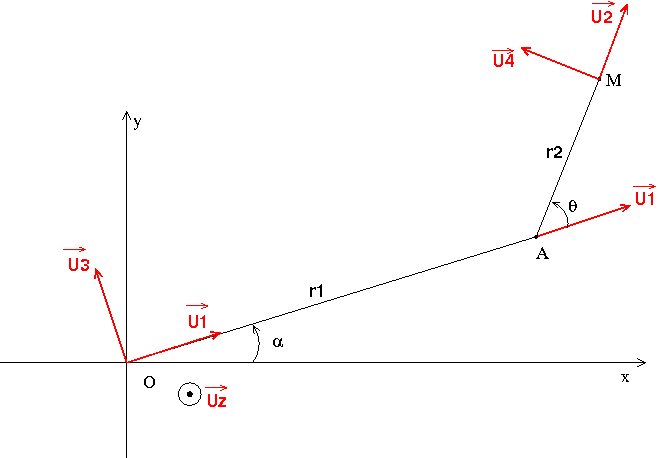
Par rapport au repère terrestre (Oxy) la tige OA de longueur r1 tourne à la vitesse angulaire 1 autour de l'axe fixe Oz perpendiculaire au plan de figure.
La tige AM de longueur r2 tourne autour d'un axe mobile (Az) de sorte que l'angle soit égal à (2t+o) et il s'agit de déterminer la norme du vecteur accélération de M par rapport à (Oxy) ?
Est-ce bien cela ? Si oui, tu as tout intérêt à utiliser la relation de composition des accélérations

Equation d\'une accélération

Posté par
Halre : Equation d'une accélération 08-09-16 à 14:03

Bonjour,

Alors oui, je pense que c'est tout a fait ca !

Personnellement, j'ai fait partir le vecteur U1 directement du point M. C'est pourquoi pour j'ai calculé la norme de l'accélération totale a partir de la somme vectorielle de U2 et U1.

Donc ceci est incorrect ?

Si c'est le cas, pourriez-vous m'aider avec la relation de composition ? J'ai vu qu c'etait la somme de l'accélération absolue, relative et d'entrainement. Est-ce bien cela ?

Merci par avance,

Hal

Posté par
Halre : Equation d'une accélération 08-09-16 à 16:18

U1 et U2 étant les accélérations centrifuges générées par la rotation des rotors correspondant.

Au final, ce que j'aimerais, c'est calculer la vitesse et la trajectoire du point M dans le référentiel du tube.

Y'a peut-etre une différence entre nos points de vues en fait. Je me place dans le référentiel du tube.

Merci par avance,

Hal

Posté par
vanoisere : Equation d'une accélération 08-09-16 à 22:34

Citation :
Y'a peut-etre une différence entre nos points de vues en fait. Je me place dans le référentiel du tube.

Pour l'étude ultérieure du liquide, il peut effectivement être intéressant de se placer dans le référentiel du tube ; mais alors, il te faudra faire intervenir les pseudo-forces d'inertie et en particulier la pseudo force d'inertie d'entraînement qui se déduit de l'accélération par rapport à la terre d'un point M fixe par rapport au tube. Donc : quel que soit le point de vue adopté pour traiter l'ensemble du problème, tu as besoin de connaître l'accélération du point M par rapport à la terre, c'est à dire par rapport au repère R : (Ox,y). Je la note \overrightarrow{a_{M/R}}, le point M étant supposé fixe par rapport au tube.
Deux méthodes sont envisageables :
1° la méthode consistant à exprimer les coordonnées du point M dans le repère terrestre R : (Oxy) en fonction de r1,r2, et puis à dériver deux fois par rapport au temps.
2° la méthode dite de composition des vitesses et des accélérations.
Pour ce problème, les deux méthodes sont sensiblement de même longueur : la première est plus simple physiquement mais plus "technique" au niveau de la trigonométrie. La seconde est plus simple au niveau des calculs mais demande plus de "sens physique". Je développe la seconde.
On définit un repère intermédiaire RT lié à la tige OA : c'est le repère \left(O,\overrightarrow{u_{1}},\overrightarrow{u_{3}},\overrightarrow{u_{z}}\right) tournant par rapport au repère terrestre R à la vitesse angulaire : \omega_{1}=\frac{d\alpha}{dt} autour de l'axe (Oz).
Le vecteur accélération absolue est la somme de trois vecteurs :

\overrightarrow{a_{M/R}}=\overrightarrow{a_{M/R_{T}}}+\overrightarrow{a_{e}}+\overrightarrow{a_{C}}
L'accélération relative \overrightarrow{a_{M/R_{T}}} est l'accélération correspondant à la rotation de M à la vitesse angulaire 2 par rapport à RT :

\overrightarrow{a_{M/R_{T}}}=-r_{2}\cdot\omega_{2}^{2}\cdot\overrightarrow{u_{2}}
L'accélération d'entraînement est l'accélération qu'aurait M par rapport à la terre si M restait immobile par rapport à RT, donc si restait fixe :

\overrightarrow{a_{e}}=-\omega_{1}^{2}\cdot\overrightarrow{OM}=-\omega_{1}^{2}\cdot\left(r_{1}\cdot\overrightarrow{u_{1}}+r_{2}\cdot\overrightarrow{u_{2}}\right)
L'accélération de Coriolis est donnée par la relation (là : il faut connaître son cours !) :

\overrightarrow{a_{C}}=2\cdot\omega_{1}\overrightarrow{u_{z}}\wedge\overrightarrow{v_{M/R_{T}}}=2\cdot\omega_{1}\overrightarrow{u_{z}}\wedge\left(r_{2}\omega_{2}\cdot\overrightarrow{u_{4}}\right)=-2\cdot r_{2}\cdot\omega_{1}\cdot\omega_{2}\cdot\overrightarrow{u_{2}}
L'accélération de M par rapport à la terre est ainsi :

\overrightarrow{a_{M/R}}=-r_{2}\cdot\omega_{2}^{2}\cdot\overrightarrow{u_{2}}-\omega_{1}^{2}\cdot\left(r_{1}\cdot\overrightarrow{u_{1}}+r_{2}\cdot\overrightarrow{u_{2}}\right)-2\cdot r_{2}\cdot\omega_{1}\cdot\omega_{2}\cdot\overrightarrow{u_{2}}=-\omega_{1}^{2}\cdot r_{1}\cdot\overrightarrow{u_{1}}-\left(\omega_{1}^{2}+\omega_{2}^{2}+2\cdot\omega_{1}\cdot\omega_{2}\right)\cdot r_{2}\cdot\overrightarrow{u_{2}}

\overrightarrow{a_{M/R}}=-\omega_{1}^{2}\cdot r_{1}\cdot\overrightarrow{u_{1}}-\left(\omega_{1}+\omega_{2}\right)^{2}\cdot r_{2}\cdot\overrightarrow{u_{2}}

\left(\overrightarrow{a_{M/R}}\right)^{2}=r_{1}^{2}\cdot\omega_{1}^{4}+r_{2}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{4}+2r_{1}\cdot r_{2}\cdot\omega_{1}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\cos\theta

\Vert\overrightarrow{a_{M/R}}\Vert=\sqrt{r_{1}^{2}\cdot\omega_{1}^{4}+r_{2}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{4}+2r_{1}\cdot r_{2}\cdot\omega_{1}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\cos\left(\omega_{2}\cdot t+\theta_{0}\right)}

Posté par
vanoisere : Equation d'une accélération 08-09-16 à 23:08

J'ai oublié de posté le schéma complété  ! Le voici :

Equation d\'une accélération

Posté par
Halre : Equation d'une accélération 09-09-16 à 01:03

Wah. Merci pour cette réponse tres détaillée !

Avant de passer a l'étape suivante avec les pseudo forces, je vais tenter de calculer l'accélération avec la premiere méthode pour voir si j'y arrive.

Je suis ingénieur en biotechnologie donc mon domaine d'expertise se trouve loin de la mécanique newtonienne

Je fais ca dans le cadre de projets annexes.

Posté par
vanoisere : Equation d'une accélération 09-09-16 à 20:30

Bonjour
Devant m'absenter d'ici quelques jours, je te poste le calcul correspondant à la détermination directe de l'accélération dans le repère terrestre R : (0,x,y,z). En posant, conformément à la figure :

\alpha=\omega_{1}\cdot t+\alpha_{0}\quad;\quad\theta=\omega_{2}\cdot t+\theta_{0}
les coordonnées du point M dans (R) à la date t sont :

\begin{cases} \\ x=r_{1}\cdot\cos\left(\alpha\right)+r_{2}\cdot\cos\left(\alpha+\theta\right)\\ \\ y=r_{1}\cdot\sin\left(\alpha\right)+r_{2}\cdot\sin\left(\alpha+\theta\right)\\ \\ z=0 \\ \end{cases}
Les coordonnées du vecteur vitesse de M dans (R) s'obtiennent en dérivant par rapport au temps :

\begin{cases} \\ v_{x}=-r_{1}\cdot\frac{d\alpha}{dt}\cdot\sin\left(\alpha\right)-r_{2}\cdot\frac{d\left(\alpha+\theta\right)}{dt}\cdot\sin\left(\alpha+\theta\right) & v_{x}=-r_{1}\cdot\omega_{1}\cdot\sin\left(\alpha\right)-r_{2}\cdot\left(\omega_{1}+\omega_{2}\right)\cdot\sin\left(\alpha+\theta\right)\\ \\ v_{y}=r_{1}\cdot\frac{d\alpha}{dt}\cdot\cos\left(\alpha\right)+r_{2}\cdot\frac{d\left(\alpha+\theta\right)}{dt}\cdot\cos\left(\alpha+\theta\right) & v_{y}=r_{1}\cdot\omega_{1}\cdot\cos\left(\alpha\right)+r_{2}\cdot\left(\omega_{1}+\omega_{2}\right)\cdot\cos\left(\alpha+\theta\right) \\ \end{cases}
Les coordonnées du vecteurs accélération de M dans (R) s'obtiennent en dérivant par rapport au temps, suivant une méthode analogue :

\begin{cases} \\ a_{x}=-r_{1}\cdot\omega_{1}^{2}\cdot\cos\left(\alpha\right)-r_{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\cos\left(\alpha+\theta\right)\\ \\ a_{y}=-r_{1}\cdot\omega_{1}^{2}\cdot\sin\left(\alpha\right)-r_{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\sin\left(\alpha+\theta\right) \\ \end{cases}
Le carré de la norme du vecteur accélération vaut :

\left(\overrightarrow{a_{M/R}}\right)^{2}=a_{x}^{2}+a_{y}^{2}
\left(\overrightarrow{a_{M/R}}\right)^{2}=r_{1}^{2}\cdot\omega_{1}^{4}\cdot\cos^{2}\left(\alpha\right)+r_{2}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{4}\cdot\cos^{2}\left(\alpha+\theta\right)+2r_{1}\cdot r_{2}\cdot\omega_{1}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\cos\left(\alpha\right)\cdot\cos\left(\alpha+\theta\right)+...
...+r_{1}^{2}\cdot\omega_{1}^{4}\cdot\sin^{2}\left(\alpha\right)+r_{2}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{4}\cdot\sin^{2}\left(\alpha+\theta\right)+2r_{1}\cdot r_{2}\cdot\omega_{1}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\sin\left(\alpha\right)\cdot\sin\left(\alpha+\theta\right)
En tenant compte de la relation entre le carré du sinus et le carré du cosinus, on obtient :

\left(\overrightarrow{a_{M/R}}\right)^{2}=r_{1}^{2}\cdot\omega_{1}^{4}+r_{2}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{4}+2r_{1}\cdot r_{2}\cdot\omega_{1}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\left[\cos\left(\alpha\right)\cdot\cos\left(\alpha+\theta\right)+\sin\left(\alpha\right)\cdot\sin\left(\alpha+\theta\right)\right]

2\cos\left(\alpha\right)\cdot\cos\left(\alpha+\theta\right)=\cos\left(2\alpha+\theta\right)+\cos\left(\theta\right)

2\sin\left(\alpha\right)\cdot\sin\left(\alpha+\theta\right)=\cos\left(\theta\right)-\cos\left(2\alpha+\theta\right)
On obtient bien (heureusement !) la même expression que par l'autre méthode :

\left(\overrightarrow{a_{M/R}}\right)^{2}=r_{1}^{2}\cdot\omega_{1}^{4}+r_{2}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{4}+2r_{1}\cdot r_{2}\cdot\omega_{1}^{2}\cdot\left(\omega_{1}+\omega_{2}\right)^{2}\cdot\cos\left(\theta\right)
Comme je te le disais précédemment : avec cette méthode : moins de physique, plus de trigo...

Posté par
Halre : Equation d'une accélération 10-09-16 à 00:04

J'allais justement envoyer un message pour dire que j'avais trouvé les coordonnées du point M et je voulais te le montrer pour vérification ! Et c'était bien ca.

Je n'avais cependant pas encore fait l'exercice mathématique. Bonne surprise donc !

Merci beaucoup pour ton implication.

Je vais me renseigner sur la partie "pseudo force".

Bon weekend !

Hal


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !