Inscription / Connexion Nouveau Sujet
Enfant fait tourner une bille au bout d'un fil autour de sa main
Bonjour,
J'ai reçu le DM suivant en MSI (mécanique du solide indéformable):
Un enfant fait tourner autour de son poignet une balle de masse m au bout d'un fil de longueur R.
Je suis bloqué à la question suivante: Déterminer la vitesse de rotation minimum pour que la balle fasse un tour complet? Faire l'application numérique suivante: m=100g et R=50cm.
Voilà ce que j'ai fait:
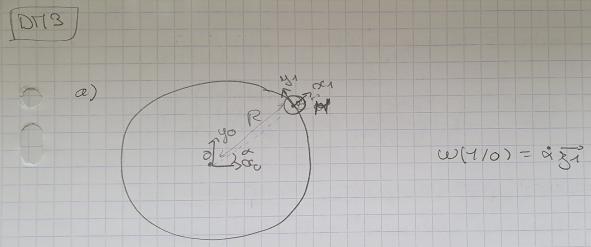
1) J'ai défini 2 repères distincts, un fixe R0 placer au centre du cercle décrit par la balle et un attaché à l'objet R1: x1 est dans le prolongement du fil (voir image en annexe). Le taux de rotation entre R1 et R0 est la dérivée première de l'angle porté par z1,0 ( car l'axe est commun au 2 repères). Soit w(1/0)= 
'*z1,0
2) J'ai défini le vecteur position OM = (0,R,0) dans R1, O centre du cercle, M centre de la balle. De la j'ai pu dériver par rapport au temps et obtenir l'expression de la vitesse et de l'accélération.
Grâce à la 2eme lois de Newton j'ai défini que -P*y0 - T*x1 =m*a. T étant la tension dans le fil.
Ce qui me donne dans R1: -mg(sin()*x1 + cos()*y1 + T*x1 = m (-R'^2*x1 +R''*y1)
J'ai donc L'expression de mes 2 accélération la tangeantielle selon y1 et la normale selon x1. On sait que l'accélération normale est également égale à (-v^2/R)*x1 car nous sommes dans un repère galliléen. De là j'ai déterminer l'expression littérale de ma vitesse : -mR'^2 =-mv^2/R 
v=R'
Après ça je suis bloquée...
Je ne sait pas comment faire l'application numérique. Comment gérer la dérivé première de mon taux de rotation. Je sais que est une fonction du temps, c'est l'angle sur le temps mais si je dériver le temps ne disparait pas ça devient -angle/t^2. Comme la question est pour un tour je suppose que mon angle ici est égale à 2pi. Dois-je prendre mes trois équations (les 2 selon x1 et une selon y1) et déterminer mes 3 inconnues? (la vitesse, le temps, et la tension dans le fil)
Je me demande si je n'aurais pas loupé quelque chose...
Merci d'avance
Bonjour
On peut se contenter de travailler dans le repère terrestre galiléen.
La méthode consiste à exprimer la tension T du fil en fonction de l'angle et de la vitesse Vo de la balle à sa position basse. On écrit ensuite que la tension ne s'annule jamais quelle que soit la valeur de l'angle et on obtient une condition sur Vo.
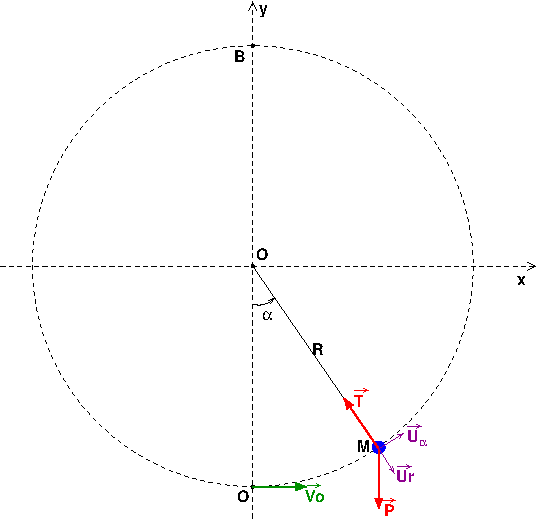
Un schéma pour illustrer mon précédent message. On suppose j'imagine, le point O fixe par rapport à la terre et le mouvement de M s'effectue dans un plan vertical.
J'ai un problème de signe.
J'ai exprimé ma tension dans R0 ainsi que l'accélération normale. L'accélération tangentiel c'est la dérivé de Vo par rapport au temps, or comme Vo est la vitesse minimal je la suppose constante sa dérivé est donc nulle.
J'obtiens selon xo/ -T*sin()=(-v^2/R)*sin()
yo/ T*cos() - m*g= (v^2/R)*cos()
J'isole T et je dis que T>0 peut importe la valeur de mais le problème est que selon yo j'obtiens : Vo^2 > -(m*g*R)/cos() .
C'est bizarre ce moins...
Il faut procéder en trois étapes :
1° appliquer le théorème de l'énergie cinétique entre la position basse de vitesse Vo et la position quelconque M de vitesse V.
1° : Tu obtiens ainsi V2 en fonction de Vo2, g,R et .
2° : Tu projettes la relation fondamentale de la dynamique suivant . Tu obtiens la norme T de la tension en fonction de m,g,R,V2 et
. Projeter suivant x et suivant y est possible mais plus long.
3° : Tu élimines V2 entre les deux relations. Il suffit alors d'écrire que T ne s'annule jamais quelle que soit la valeur de et cela te donne la condition recherchée sur Vo.
Je ne suis pas sure d'avoir bien compris l'étape 2. C'est un peu flou.
J'ai fait l'étape une et j'ai obtenu v^2 = Vo^2 - 2gRcos()
Etape 2 deuxième lois de newton et j'ai tout exprimé suivant vect(Ur):
-T - mgcos()=m*ur
-T - mgcos()=m*(-v^2)/R
T = m(v^2/R - gcos())
De la Etape 3 T>0, m(v^2/R - gcos()) >0, ma masse disparait (est-ce normale? ), en remplaçant par la v^2 par la première étape je trouve que Vo^2> 3Rgcos().
Pour faire un tour = 2pi, R=0,5m
Vo= 3,84 m/s
Est ce logique?
Parce que j'ai aussi fait mais en projetant tout dans Ro et là j'obtions une équation pour vo avec la masse m. Vo> racine ( mgR/cos() + 2gRcos())
Est- ce plus logique?
Il y a quelques erreurs.
L'augmentation d'altitude entre le point bas de la trajectoire et le point M est :
Tu aurais pû tester ta formule dans des cas simples évidents : =0 ou =
/2 ; tu aurais facilement ainsi compris que ton expression est fausse.
L'accélération normale est centripète. La projection de la RFD suivant donne :
Je te laisse corriger la suite...
Merci beaucoup, j'ai compris.
De la après j'obtiens l'expression suivante: vo^2> 2gR-3gRcos()
Je cherche pur quelle valeur de vo^2 est max, soit pi. Donc Vo=racine(5gR)
avec mes valeurs 4,95m/s
Annuler
connectez vous