Inscription / Connexion Nouveau Sujet
Énergies et mouvement circulaire
Bonjour je bloque et je ne suis pas sûr de moi sur cet exercice, pouvez-vous m'aidez s'il vous plaît?
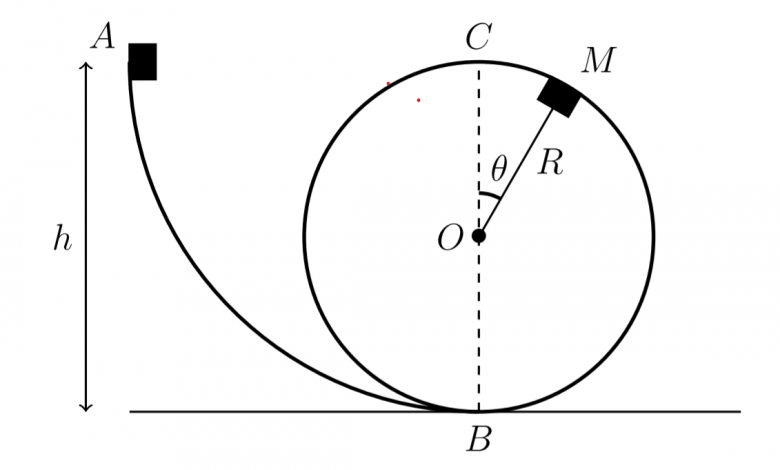
Je vous joint la figure.
1. Un solide de masse m, considéré comme un point matériel, est lâché sans vitesse
initiale d'un point A à une hauteur h le long d'un guide le menant à B. Le mouvement se fait sans frottement et l'énergie potentielle est choisie nulle en B.
(a) Faire le bilan des forces s'exerçant sur le solide pendant le parcours de A à B et les représenter sur un schéma.
(b) Déterminer le travail de chaque force entre les points A et B. A l'aide du théorème de l'énergie cinétique, donner l'expression de Ec(B) en fonction de m, g et h. En déduire la vitesse vB au point B.
2. Le solide arrive en B avec une vitesse vB et monte jusqu'au point M quelconque repéré
par l'angle θ.
(a) Faire le bilan des forces s'exerçant sur le solide au point M et les représenter sur un schéma.
(b) Déterminer le travail de chaque force entre les points B et M. En déduire l'expression de Ec(M), l'énergie cinétique en M. En déduire la vitesse vM au point M.
(c) Déterminer l'expression de l'énergie potentielle Ep(M).
(d) Calculer l'énergie mécanique totale ET aux points A, B et M. Discuter du résultat.
(e) Tracer sur un même graphe, les variations de Ec, Ep, ET en fonction de θ.
3. On s'intéresse maintenant à la force de réaction du support
au point M.
(a) Exprimer sa norme .
(b) Montrer que s'annule en un point M0 (angle θ0) vérifiant cos θ0 =
.Que se passe-t-il physiquement quand
s'annule ? Quelle est la condition sur
pour que cos θ0 < 1 ?
(c) Déterminer l'expression de v2
M0, le carré de la vitesse du solide en M0 ? Quelle est la condition que doit satisfaire pour que vM0 soit définie ?
4. Décrire qualitativement le mouvement du solide dans les trois cas suivants :
(a) h < R
(b) R < h < 5R/2
(c) h > 5R/2
Mes réponses :
1
a) Les forces exercés sont le poids noté , et la réaction au support noté
.(je ne suis pas sûr)
b) On calcule le travail des forces du point A vers le point B, on prend B = 0 et A = h.
Soit ,
On calcule Ec(B), soit
Donc
donc
2)
a) Le bilan des forces au point M :
Le poids et la réaction au support.
b) On prend comme tout à l'heure B = 0 et M = R(1+ cos θ)
Je ne sais pas je dirai 0,
On calcule Ec(M), soit
Donc
donc
c) Je ne vois pas comment calculer l'énergie potentielle
d) Énergie mécanique = énergie cinétique + énergie potentielle
e) Je ne vois pas comment représenter ce schéma
3 et 4 je ne vois pas comment faire...
Je sais que cette exercice est loin, et je tiens donc à vous remercier si vous avez déjà tout lu, et je vous remercie aussi d'avance pour toute l'aide que vous m'apporterez.
Bonsoir,
1) oui
Il n'y a pas de frottement, donc la reaction du support est ...
peux-tu poster le schema?
1b)
on prend B=0 et A=h
Ca ne veut rien dire.
Il faut definir la verticale ascendante (Bz) par ex.
Puis ecrire: zB=0 (car Epp(B) =0 par hypothese)
zA = h
Attention!
W(P)
P.AB car P et AB n'ont pas la meme direction!
En revance , oui, W(P)= mg( zA-zB) = mgh
Pourquoi W(N) = 0 ?
2) gros pb avec l'Ec negative !!!!
krinn
Il n'y a pas de frottement, donc la reaction du support est nulle
Pourquoi W(N) = 0 [\quote]
Dans votre message j'ai répondu, ci-joit vous aurez le schéma des bilans des forces de la question 1 et 2.
Pourquoi
2 je ne vois pas comment rectifier l'erreur.... Pouvez-vous m'aidez?
Je ne sais pas pourquoi WN = 0, je ne faisais qu'une hypothèse car il n'y a pas de frottement donc la réaction au support est nulle et donc il n'y a pas de travail pour cette force.
Je ne sais pas pourquoi WN = 0, je ne faisais qu'une hypothèse car il n'y a pas de frottement donc la réaction au support est nulle normale au support et donc il n'y a pas de travail pour cette force.
La reaction du support existe dès qu'il y a contact !
Donc ici tant que M reste en contact avec la piste
2) que dit le theoreme de l'Ec entre B et M ?
La réaction du support étant normale au support, alors sa norme est nulle, c'est ça?
2) Énergie cinétique (M) - Énergie cinétique (B) = W(somme des forces)
J'ai déjà calculer Énergie cinétique (B), cela vaut et je ne vois pas comment allez plus loin
La réaction du support étant normale au support, alors sa norme est nulle, c'est ça?
Non, la reaction du support N n'est pas le vecteur nul (tant qu il y a contact). Donc sa norme ne l'est pas non plus.
Mais ici c'est un vecteur perpendiculaire à la trajectoire (à tout instant t) car il n'y a pas de frottement, et donc son travail est nul (car N est tjs orthogonal au deplacement)
2) Énergie cinétique (M) - Énergie cinétique (B) = W(somme des forces)
J'ai déjà calculer Énergie cinétique (B), cela vaut
Oui, donc 1/2 m VM2 - ..... = ....
Non
Je ne comprends pas ce que tu fais.
W(P) ne vaut pas mgh dans la question 2.
Tu l'avais pourtant bien calculé dans ton 1er message
Oh oui pardon j'ai pensé à Ec(B) et donc j'ai mis la somme des forces qui allez avec excusez moi je recommence...
On simplifie par m et on multiplie par 2:
On isole vM :
Or vB² = 2gh, Soit
==>
Normalement je ne me suis pas tromper...
Il y a un - devant R(1+cos
) et il est important.
donc
Oui je l'ai marqué sur ma feuille, j'ai mal recopié pardon
donc
par def. Epp(M) = m....
Epp(M) = mg
Sans vous mentir je n'ai pas très bien compris cette partie du cours, alors pouvez-vous m'expliquer s'il vous plaît?
Il faut revoir ca.
Par definition, pour une force conservative, on a entre 2 points de la trajectoire: W(F) = -
Epp
Donc pour la pesanteur on trouve ici:
Epp(M) = mg(zM - zB) puisque l'origine de l'Epp est prise en B.
Il faut revoir ca.
Par definition, pour une force conservative, on a entre 2 points de la trajectoire: W(F) = -
Epp
Donc pour la pesanteur on trouve ici:
Epp(M) = mg(zM - zB) puisque l'origine de l'Epp est prise en B.
Donc si j'ai bien
Epp(M) = mg(R(1 + cos
- 0))
==>Epp(M) = mgR(1 + cos
) Je vous remercie 
Pour la question d) on sait que l'énergie mécanique est égale à la somme de l'énergie cinétique et de l'énergie potentielle
Donc au point M
ET(M) = Ec(M) + Epp(M)
ET(M) = Ec(M) + mgR(1 + cos)
Mais je ne sais pas à quoi correspond Ec(M),
Pour le point B
ET(B) = Ec(B) + Epp(B)
Je sais donc trouver l'énergie potentielle en appliquant le même procédé que pour M mais pas la cinétique
Pour le point A
ET(A) = Ec(A) + Epp(A)
Je ne sais pas comment calculer ET
Tu ne sais plus ce qu'est Ec(M) !!?? mais tu l'as pourtant deja utilisé dans le 2) non?
Et les autres Ec aussi.
J'avoue que j'ai un peu de mal à te suivre.
Il faut evidemment réutiliser ce que tu as trouvé dans les questions precedentes!
Dans les questions précédentes j'ai calculer Ec qui vaut....
Je viens de comprendre ma bêtise énorme....
Oui bien sûr que je connais l'énergie cinétique des trois points,
Par contre je ne vois pas comment calculer l'énergie potentielle du point A....
Donc au point M
ET(M) = Ec(M) + Epp(M)
ET(M) = 1/2mvM² + mgR(1 + cos)
ET(M) = 1/2m*(-2gR(1 + cos)+ vB²) + mgR(1 + cos)
ET(M) = 1/2m*(-2gR(1 + cos)+ 2gh) + mgR(1 + cos)
ET(M) = 1/2m*(2g(-R(1 + cos)+ h)) + mgR(1 + cos)
Pour le point B
ET(B) = Ec(B) + Epp(B)
ET(B) = 1/2mvB² + mg(0 - h)
ET(B) = 1/2m2gh - mgh
ET(B) = mgh - mgh = 0
Pour le point A
ET(A) = Ec(A) + Epp(A)
ET(A) = 1/2mvA² + Epp(A)
Pour le point A je ne vois pas comment allez plus loin...
Tu n'as pas bien compris que l'Ep ne depend que de la position d'une facon generale, et ici l'Epp ne depend que de l'altitude
Epp (M) = mg(zM -zB) = mgzM car zB=0
pour TOUT point M, donc aussi A par ex.
De plus Epp(B)=... par hypothese (origine de l'Epp en B), d'ailleurs on le retrouve par la formule.
D'autre part on lâche le corps en A sans vitesse initiale donc...
ET(M) se simplifie
Les autres sont a revoir
Je n'ai pas très bien compris pour le point M....
Pour le point B, ET n'est pas nulle? je me suis trompé?
Pour le point A, on sait qu'il n'y a pas de vitesse initiale donc l'énergie cinétique est nulle, donc ET (A) = Ep (A)
C'est cela ?
Pour M, il faut simplifier ET(M)
En B: que vaut Epp(B) ?
En A: que vaut Epp(A) ?
L'Epp (energie potentielle de pesanteur) est deja vue au lycée, non? Je ne comprends pas ce qui te bloque.
Non je ne l'ai pas vu au lycée car j'ai eu la réforme donc je devais choisir des spécialités et en terminale je n'ai pas pris physique, voilà une des raisons je pense pour laquelle je bloque.
J'ai juste une question là, qu'elle est la différence entre Ep (l'énergie potentielle) et Epp, si ça se trouve j'ai calculé la mauvaise chose pour B car j'avais fais, Ep(B) = -mgh
L'Ep est le concept general associé à toute force conservative
Et pour chaque interaction conservative on definit une Ep particuliere, par ex. l'Epp si le systeme est dans un champ de pesanteur.
Ici Ep = Epp car il n'y a que la pesanteur comme force conservative.
(mais on peut aussi definir une Ep elastique, electrique etc. en fct des situations physiques)
Et pour la pesanteur, en tout point Q on a:
Epp(Q) = mg zQ
car Epp(B)=0 et zB=0 par hypothese (on dit que origine de l'Epp est en B)
Et Epp(A) = mg zA = ...
Il faut que tu revois ton cours, je ne peux pas tout reexpliquer.
Tu peux aussi consulter nos fiches de 1ere et de terminale sur la mecanique.
Je vous remercie je pense avoir compris maintenant je comprends que vous ne puissiez tout me réexpliquer, et c'est normal. Je vais lire cette fiche car je ne comprends pas comment cela est expliquer dans mon cours.
Mais si j'ai compris ce que vous venez de m'expliquer,
Pour le point B,
ET = 1/2m*2gh + 0, car zB = 0 donc l'énergie potentielle est nulle.
Donc ET = mgh
Pour le point A, l'énergie cinétique car la vitesse initiale est nulle, de plus zA = h
donc ET = 0 + mgh = mgh
Pour le point M
ET(M) = 1/2m*(2g(-R(1 + cos)+ h)) + mgR(1 + cos)
ET(M) = mg(-R(1 + cos)+ h)) + mgR(1 + cos)
ET(M) = mg(-R(1 + cos)+ h+ R(1 + cos))
R(1 + cos) se simplifie il reste
ET(M) =mgh
Donc ET(A) = ET(B) = ET(M) ce qui est normal car il n'y a pas de frottement donc énergie mécanique est une constante.
J'espère cette voici avoir compris, en tout cas je te tiens à vous remercie de votre temps, de votre patience ainsi que de votre aide
Après je dois représenter les énergies mécanique, cinétique et potentielle sur un schéma or dans mon cours on ne nous explique pas comment nous y prendre...
Pouvez-vous m'aidez s'il vous plaît?
Donc ET(A) = ET(B) = ET(M) ce qui est normal car il n'y a pas de frottement donc énergie mécanique est une constante.
pas tout à fait.
Le système est soumis:
- à son poids qui est conservatif
- et à la réaction du support, non conservative, mais qui est normale (car pas de frottement) et donc qui ne travaille pas
donc le système est conservatif (=l'énergie mécanique du système se conserve)
C'est expliqué dans cette fiche:
[lien]
Le chap. III notamment.
2e) pour M, il faut tracer les fonctions pour
dans [0, 2
] par ex.
Ec (
) = .....
Ep(
) = mgR(1 + cos )
et ET(
) = mgh (facile! c'est une fonction constante)
comme on fait en maths avec une fonction f(x)
Bonjour @krinn,
Cela fais un jour que je cherche Ec()...Mais je ne sais pas comment le trouver, après j'ai essayer de tracer pour me donner une idée, donc ET est une droite constante donc on trace la droite y = mgh
Ensuite je sais que Ep = mgR(1 +cos) car je l'ai calculer pour le point M.
Je sais juste qu' au point A l'énergie cinétique est nulle et donc l'énergie potentielle = énergie mécanique.
Je sais aussi que l'énergie cinétique se trouve en faisant énergie mécanique - énergie potentielle. Soit
Ec = mgh - mgR(1 + cos
Ec = mg(h - R(1 + cos) mais je ne vois pas comment simplifier plus...
Et je ne sais pas si c'est la meilleur manière de trouver Ec
Pouvez-vous de m'aidez s'il vous plaît?
Oui, mais tu avais deja calculé Ec(M) dans la question 2b)
Et effectivement, Ec =ET - Epp = mgh - Epp
Donc si tu connais Epp, tu en deduis Ec facilement
Je ne comprend pas pourquoi, on doit prendre Ec, du point M, car ce qu'on veux c'est tracer les énergies cinétique, potentielle et mécanique en fonction de , or Ec(M) = 1/2mvM²
Il n'y a donc aucune intervention de,
C'est donc pour cela que j'ai écris dan smon message précédant celui ci
Je sais aussi que l'énergie cinétique se trouve en faisant énergie mécanique - énergie potentielle. Soit
Ec = mgh - mgR(1 + cos
Ec = mg(h - R(1 + cos)) mais je ne vois pas comment simplifier plus...
Et donc après pour tracer, donc je trace en y= mgh pour ET, et après je sais que "l'énergie potentielle et cinétique sont inverse l'une de l'autre", ce que je veux dire, c'est en reprenant l'énoncé, au point A on lâche l'objet sans vitesse initiale, donc pas de vitesse = pas d'énergie cinétique or l'énergie mécanique reste constante donc l'énergie potentielle = énergie mécanique, quand on suit le parcours jusqu'au point B, l'objet a pris de la vitesse donc l'énergie cinétique et potentielle s'équilibre pour toujours avoir une énergie mécanique constante. Mais je ne sais pas, en tout cas je ne sais pas comment faire faut t'il tracer les énergies cinétique et potentielle de la forme de la courbe de la valeur absolue ou alors comme celle d'un cosinus?
On demande Ec(M) qui depend de , comme Epp(M) et VM aussi
Tu l'as meme ecrit plus haut!
Ec(M) = mgh - Epp(M) = mgh - ...
Donc il faut representer Epp() qui est un simple cosinus "decalé vers le haut"
Puis Ec ()
A ne nous interesse pas ici, on ne s'interesse qu'aux points M sur le cercle
Non
Ec(M) = mgh -mgR(1 +cos)
Epp(M) = mgR(1 +cos)
franchement, je ne comprends pas ce que tu fais, tu l'avais ecrit correctement à 15h10 , non?
Au final c'est que j'ai mal compris votre message, et donc je pensais que ce que j'avais écris dans le message de 15h10 était faux donc je cherchais un autre résultat, tout simplement. Excusez moi si je suis un peu incompréhensible.
Mais même avec le bon résultat je ne vois pas comment tracer l'énergie potentielle et cinétique.... Je sais juste qu'elles sont complémentaire.
Ok, donc M est un point courant repéré par et on a:
Ec(M) = mgh -mgR(1 +cos)
Epp(M) = mgR(1 +cos)
Pour le tracé, tu prends h>R par ex., tu pars de Ep, tuconnais l'allure de y=1+cos() donc tu traces qqes points caracteristiques (pour =0, /2, ,...)
Et ensuite comme Ec = mgh -Epp on en deduit facilement son allure, aussi
Voir figure( à completer).
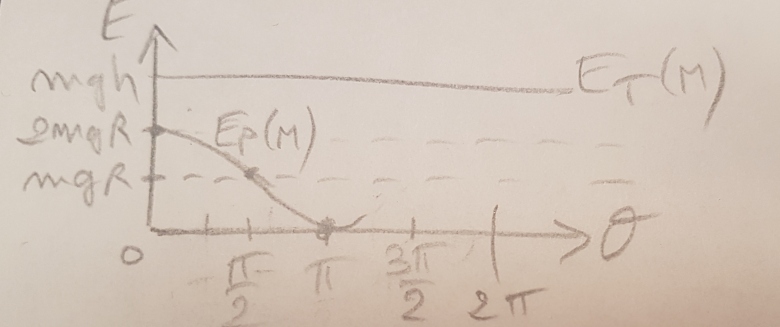
Bonjour, grâce à votre graphique j'ai compris.
Voici le mien ci-joint.
Désolé c'est mon brouillon, il est un peu sale j'ai recommencé 2-3 fois.
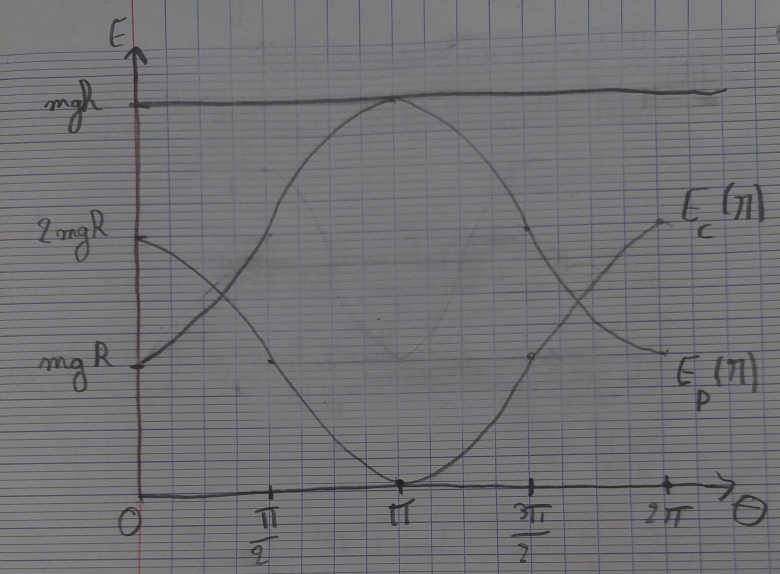
oups, oui excusez moi.
Sinon cela est juste ?
Je vous remercie pour l'aide et le temps que vous m'avez accordé.
Annuler
connectez vous