Bonsoir,

  Je voudrais me corriger  concernant l'expression de l'énergie potentielle dans deux cas, figure a et figure b :

Données liées à la figure a :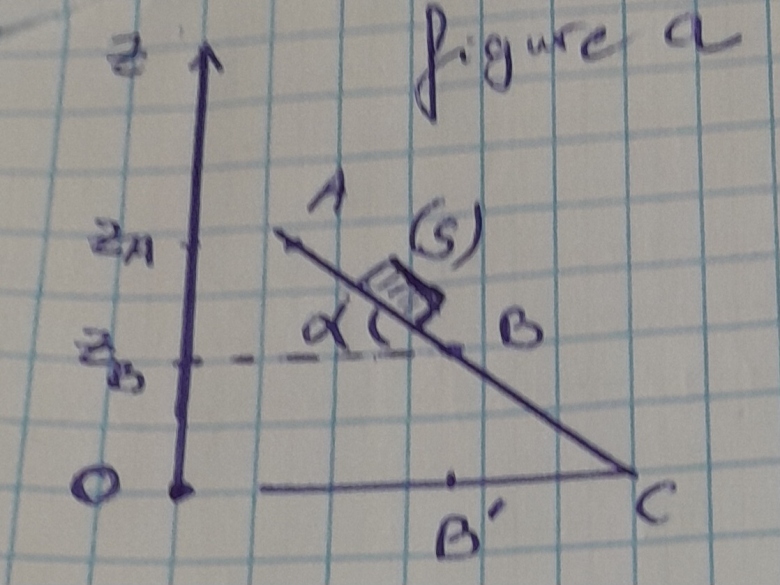





On considère le plan horizontal passant par le point B comme état de référence de l'énergie  potentielle de pesanteur (E_pp); et le point O comme origine de l'axe des côtes, orienté vers le haut,

Montrer que l'expression de E_pp est :  E_pp=m.g.(z-BCsin())

Réponse pour ce cas :

  Par définition  E_pp= m.g.z + C,
La valeur de la constante C est liée  à l'état référentiel.

Ici E_pp=0 quand (S) est en B de côte z_B > 0, donc on peut écrire :  0= m.g.z_B+C.

C= -m.g.z_B , or z_B>0 est correspond à la hauteur BB', B' étant le projeté orthogonal du point B sur  (OC) et donc z_B=BB'=BC .sin ,

En remplaçant dans l'expression générale  définissant  E_pp,

E_pp= m.g.(z-BC.sin)

Données  en relation avec la figure b :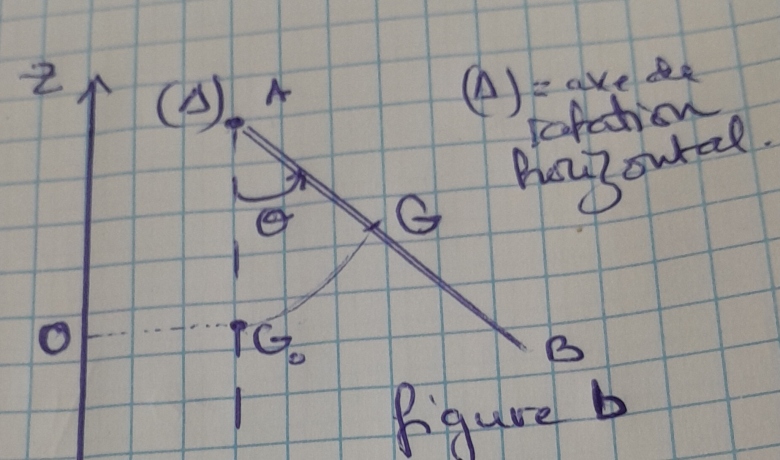



On considère la position d'équilibre stable comme état de référence de l'énergie potentielle de pesanteur.  La position de la barre est définie par.
On écarte la barre de sa position d'équilibre d'un angle _m=60° et on la lâche sans vitesse initiale,

Établir l'expression d'E_pp à un instant où la position de la barre est repérée par une abscisse angulaire quelconque.


Réponse  liée à ce cas de figure :

E_pp= m.g.z + C .
Ici quand E_pp=0 ;  z=z_Go=0  ( car le centre de gravité de la barre coïncide avec O le point de côte nulle  sur l'axe des côtes),

Donc  E_pp=0= m.g.z_Go+C   donc  0=0+C, d,où on peut écrire dans les conditions sus-citées que E_pp= m.g.z

Merci par avance.
Je voudrais des précisions si mes réponses sont insuffisantes.
Merci encore.

_{malou edit > ** ai replacé les figures**}