Inscription / Connexion Nouveau Sujet
Energie Mécanique (Mécanique du point)
Bonsoir à toutes et à tous !
Voilà, je bloque sur un exercice de Mécanique du point
J'ai réussi les premières parties mais je bloque sur la dernière.
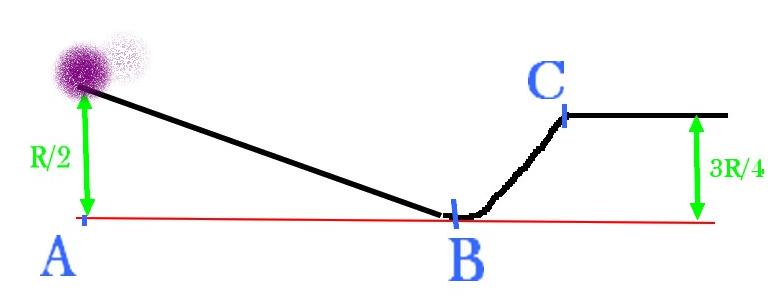
Enoncé:
Une balle de masse m, considéré comme un point se déplace sans frontement sur la rampe.
Vitesse initiale est V0= Sqrt(2*g*R)
a) Avec quelle vitesse et quel angle par rapport à la verticale la balle quitte la rampe en en c ? (pour la suite, on posera à cet instant à t=0s)
b) Equation paramétrique du mouvement+équation de la trajectoire à partir de t=0s.
c) A quelle Distance du point B faut il placer un panier pour récupérer la balle ?
Ce que je connais d'après les questions précédentes et qui pourrait être utile
* Il y a conservation de l'énergie mécanique en tout point de la rampe
Voici mon raisonnement:
a) Pour la vitesse, j'utilise le principe de conservation en A et C
Em(c)=Em(a)
Ecc(c)+Epp(c)=Ecc(a)+Epp(a)
0.5*vc²+g*(3R/4)=0.5*v0²+R/2 (j'ai simplifié par m)
V(c)=(3/4)*sqrt(Rg)
Je pense que c'est correct mais je bloque pour l'angle. Je ne connais aucune formule permettant de le déterminer et je ne vois pas d'amorces dans l'énoncé qui m'aiderait à commencer.
b)J'utilise l'énoncé
Soit Vc au point C et vz la vitesse selon l'axe verticale
Vz=vc donc z=vc*t+Constante
or à t=0s, z=3R/4 d'après le schéma.
Donc z= Vc*t+ (3R/4).
Les autres composantes (x,y) sont nulles.
C'est pourquoi, je coince sur la trajectoire car je sais qu'on l'obtient en éliminant le paramètre t mais ici je ne sais comment faire avec une seule équation.
3) Difficile, je trouve. Je pensais à calculer la portée, non ? Mais il me faut plus d'équations pour ça ce qui pose problème.
Merci de votre aide.
Je précise que le rond violet est la balle
Je me sens d'humeur taquine.
Je pose donc la question : La boule roule t'elle sans glisser ou glisse t'elle sans rouler ?
Il ne faut pas penser que ceci est une question anodine (même si le rayon de la boule tend vers 0)
Et dans le cas où la boule roule, alors la boule est-elle pleine et homogène ? (même si elle est réduite en un point).
-----
Il est fort probable que ces questions n'ont pas effleuré l'auteur de la question et pourtant :
Supposons une boule de rayon R dont le ventre d'inertie à une vitesse v, si la boule boule sa vitesse angulaire est w = v/R
L'énergie cinétique de translation de la boule est (1/2).m.v²
L'énergie cinétique de rotation de la boule est (1/2).J.w²
Et si la boule est pleine et homogène: J = (2/5).m.R², on a alors l'énergie cinétique de rotation de la boule est (1/2)*(2/5).m.R²*v²/R² = 0,2. mv²
... Et donc l'énergie cinétique totale de la boule est Ec = (1/2).m.v² + 0,2. mv² = 0,7.mv² (et ceci pour une masse donnée, et quel que soit R, donc même si R --> 0)
-----
Mais je mettrais volontiers ta tête à couper que le prof n'a jamais pensé à ce genre de problème...
Remarque que s'il n'y a aucun frottement il serait étonnant que la boule roule sans glisser.
Par contre, s'il faut comprendre "sans pertes due au frottement", alors la boule pourrait bien rouler.
-----
Pour ton problème:
L'angle à prendre en considération lorsque la boule quitte la piste en C est imposé par la pente en C de la portion BC de la piste.
Mais il manque au moins une donnée pour pouvoir la calculer (par exemple dire que BC est une droite et qu'on connaisse la distance horizontale séparant B et C)
-----



