Bonjour,

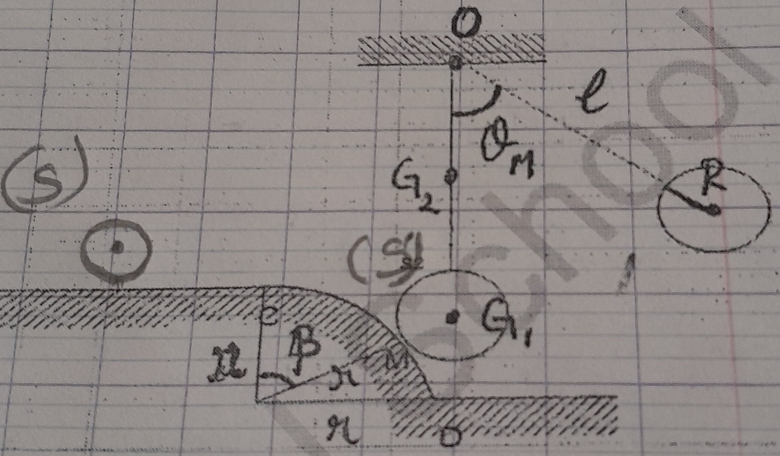
   un pendule (S') constitué d'un corps sphérique de masse m₁=300g ,  de rayon R=5cm, suspendu à une tige métallique de longueur l=25cm et de masse m₂=150g, peut tourner sans frottement autour d'un axe de rotation O (figure ci-jointe).
On donne g=10N/kg.

  Au point M, le corps (S) dont  V_M=2,31m/s et sa masse m =400g, heurte le corp(S') au repos, en lui communiquant 35% de son énergie cinétique.

1. Déterminer v' la vitesse du corps (S')au point M. (v'est la vitesse de la partie sphérique).
2.exprimer E_ppmax (l'énergie potentielle de pesanteur maximale) du pendule en fonction de  :

;  sachant que la position initiale du pendule est considérée comme état de référence de l'énergie potentielle (E_ppM=0J).

3. En  appliquant  le théorème de conservation d'énergie entre la position M et  la position d'arrêt de la pendule repérée par  _M, déterminer la mesure de cet angle.




Réponse  :  

1. la vitesse au point M :  .
  
A.N :  v'=1,58m/s

2.  On  doit chercher d'abord la position du barycentre  du système représenté par la tige métallique et la  sphère :
  
en utilisant la relation caractéristique du barycentre ,  on prouve que O, G₁, G₂et G sont alignés et tous sur la tige métallique ,  
.
      

OG= 24,16 cm  donc à 0,84cm  de la surface de la sphère   et  sur la tige .
  
  donc  E_PP= m₂.g.Z +C,  en tenant compte des données  E_pp=m₂.g.z -m₂g.z₀.

  
  donc E_pp=m₂.g.h_G.

Donc  E_ppmax=m₂.g.h_Gmax

  

3. valeur  de  _M à la position d'arrêt :

   En appliquant le théorème de conservation d'énergie(absence des frottements), on peut écrire :  E_m=E_c+E_pp et E_m=E_cmax= E_ppmax.


Après je suis dans le doute :  

    l'énergie cinétique max est celle qu'avait la sphère au point M c'est a dire   0,5m₁v'²    et   E_ppmax = m'gOG. (1-cos max).

et je me demande si m'= m₁+m₂ ou je prends seulement m'=m₂ le poids de la tige car G du système est situé sur cette tige .

et donc je suis bloqué  à partir de la question 2 .

Merci par avance de me préciser la bonne réponse .