Inscription / Connexion Nouveau Sujet
Énergie cinétique
Salut tout le monde j'ai un exo que ne parviens pas résoudre à partir de la deuxième question pouvez m'aider svp ...
On considère un disque plein homogène de masse M=100g de rayon R=20cm et de Centre c
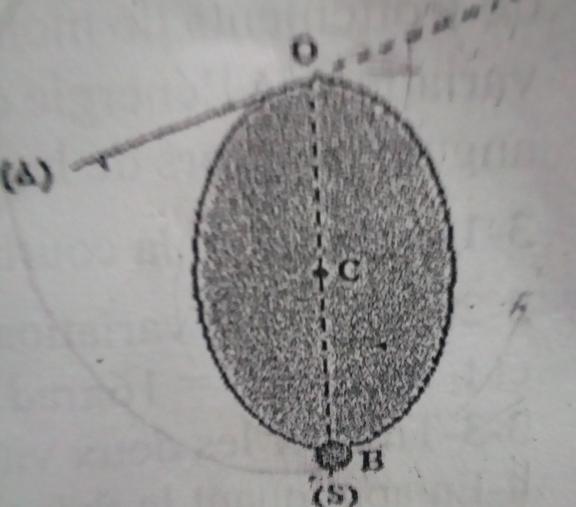
1/ le disque peut osciller dans un plan vertical autour d'un axe horizontal fixe ∆ perpendiculaire à son plan et passant par un point O de sa circonférence v. Au point B diamétralement opposé à O on fixe une sphère S assimilable a un corps ponctuel de masse m= M/2
1.1 Montrer que la distance du centre d'inertie G du système disque plus corps à l'axe ∆ est OG=a=(4/3R)
1.2 Montrer que le moment d'inertie du système par rapport à l'axe ∆ est J∆ =7mR²
2 . Quelle vitesse minimale faut il communiquer au point B lorsque le disque est dans sa position d'équilibre stable pour qu'elle effectue un tour complet autour de l'axe ∆
3. On enlève le corps S on fait tourner le disque seul à l'aide d'un moteur . Lorsque le disque atteint la vitesse de rotation égale à 300tours/ min et on applique sur le disque un couple de freinage de moment M constant . Il s'arrête après avoir effectué 250 tours compte à partir de l'arrêt du moteur . Calculer le moment du couple de freinage.
Donc j'ai trouvé les deux premières questions 1.1 et 1.2 mais je comprends pas cette notion de vitesse minimale
Bonjour
Qu'as-tu réussi à faire pour l'instant ? Qu'est-ce qui te bloque exactement ?
Pour la question 2 : tu peux appliquer le théorème de l'énergie cinétique entre l'instant initial et l'instant correspondant à une rotation d'un demi tour, sachant que dans ce dernier cas, l'énergie cinétique doit être positive ou dans le cas limite nulle.
le moment d'inertie du système par rapport à l'axe ∆ est J∆ =7mR²
Étourderie de recopie de l'énoncé peut-être...Es-tu bien sûr de l'expression de J
 ?
?J'ai réussi à l'aide de la notion de barycentre à trouver oG= 4R/3 et J∆ = 7mR² à partir de là si j'applique le Tec du point B à un point M sur le demi cercle que décrit le système j'ai
1/2 MVm²- 1/2 MVb² = mgrπ mais on ne connait pas le volume de B
D'accord avec ton expression de a=OG mais Il te faut revoir ton calcul de moment d'inertie.
Ensuite, tu peux déterminer l'expression de l'énergie cinétique du solide de masse (3M/2) lorsque le point B est en position basse avec une vitesse Vo.
Tu peux ensuite calculer le travail des forces appliquées à ce solide entre cette situation initiale et un situation où B est en position haute....
Aide-toi éventuellement d'un schéma
La valeur minimale de Vo demandée correspond au cas limite où B se retrouve en position haute avec une énergie cinétique nulle.
Merci pour le schéma ; le moment d'inertie du disque homogène de masse M par rapport à un axe parallèle à  passant par C est :
passant par C est :
Le théorème de Huygens appliqué à ce disque permet d'obtenir le moment d'inertie du disque par rapport à l'axe  :
:
Le solide (S) quasi ponctuel de masse (M/2) est à la distance 2R de l'axe de rotation ; son moment d'inertie vaut :
Le moment d'inertie de l'ensemble est :
Je te laisse conclure...
Pourquoi dans ces conditions avoir dit dès le début : "j'ai réussi à trouver J = 7M.R2 " ?
= 7M.R2 " ?
En notant Vo (provisoirement inconnue) la vitesse du point B lorsque ce point B est à sa position d'équilibre stable (position la plus basse), peux-tu exprimer l'énergie cinétique du solide dans cette position que l'on considère comme la position initiale ?
L'application du théorème de l'énergie cinétique va ensuite permettre d'obtenir la valeur de Vo comme déjà expliqué.
Tu postes au niveau première mais je ne suis pas sûr que cet exercice corresponde à ce niveau. Cet exercice a été donné par ton professeur ou tu l'as trouvé sur un livre d'exercice ?
1- Connais-tu l'expression générale de l'énergie cinétique d'un solide en rotation autour d'un axe fixe ?
2- Connais-tu l'expression générale du théorème de l'énergie cinétique ?
3- Connais-tu l'expression du travail de la force de pesanteur ?
Si tu peux répondre honnêtement oui à chacune de ces trois questions, reprendre pas à pas mes messages précédents devrait te permettre d'avancer.
Si la réponse est non : commence par bien revoir le cours correspondant avant d'essayer de résoudre l'exercice. Je ne vois pas ce que je pourrais ajouter sans te fournir directement la réponse.