Inscription / Connexion Nouveau Sujet
Energie cinétique
Bonjour, j'ai un petit problème avec les dernières questions
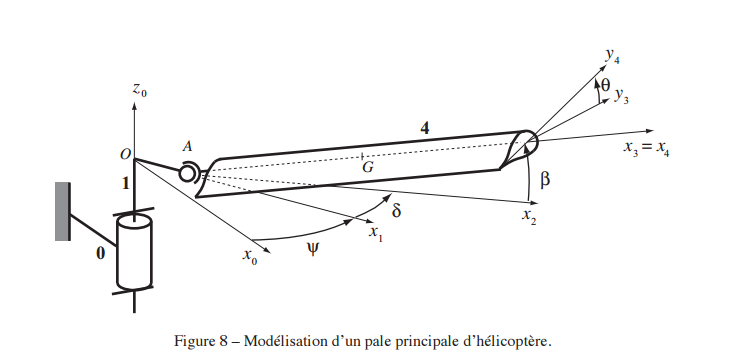
On s'intéresse à la modélisation d'une pale du rotor principal d'hélicoptère, présentée Figure 8. Le référentiel de l'hélicoptère est noté R0 et est muni d'un repère (O,x0,y0,z0). Le référentiel R0 est confondu avec le référentiel terrestre Rg.
Le moyeu principal 1 tourne autour de l'axe (O,z0) à la vitesse constante Ω telle que Ω = ψ' . La liaison entre la pale 4 et le moyeu 1 est modélisée par une rotule de centre A.
La distance OA est notée e. La longueur de la pale est notée L et son centre de gravité G. On a en particulier AG = L/2. On fait l'hypothèse que l'opérateur d'inertie de la pale exprimé au point G s'écrit sous la forme :
Hélicoptère de masse totale M et muni d'un rotor comportant Npales pales équi-réparties, chacune de masse m
D)L'énergie cinétique de l'hélicoptère dans son mouvement par rapport à Rg, en incluant lespales, peut s'écrire :
(1/2)M*(Z')² +(Npales/2)(C +m(e+L/2)²)Ω²
En fait je vois pas ccomment arriver la (Npales/2)(C +m(e+L/2)²)Ω²
Merci