Inscription / Connexion Nouveau Sujet
Electrostatique : recherche d'équipotentiel nulle
Bonjour à tous, cet exercice me pose probleme :
En deux points A et B de l'espace sont disposées les charges electriques suivantes : une charge q positive au point A et une charge négative -
q au point b.
On désigne par d la distance entre AB, et 0<<1.
Un point P de l'espace est défini par PA=r et PB= r'.
1)Definir le potentiel electrostatique au point P (avec V=0 à l'infini)
2)Montrer que la surface equipotentielle de potentiel nul est une sphere S ou l'on determinera son centre O et son rayon R ; calculer a = et R en fonction de
et d.
3) Determiner en fonction de q, d, r et le champ electrostatique resultant cree par les charges precedentes en u point P de la sphere S.
J'ai passé du temps sur cet exo (je ne suis pas tres bon en electrostat'), à la 1) j'ai trouvé :
V = (q(r'-r)/(4
0rr')
Pour la 2), il faut donc avoir : r' = r, mais je n'arrive pas a aller plus loin ...
Je vous demande donc de l'aide sur cette question.
Merci d'avance.
Bonsoir. Je suis d'accord jusque là.
Considère, sur la droite AB où se trouveront les deux points P. Tu trouveras alors le centre O, sur (AB)
J'avance un peu...
le point sur [AB]:
r(+1)=d
r=d/(+1)
le point à l'extérieur de AB, du coté de B (<1)
r=d+r
r=d/(1-)
on fait la moyenne pour trouver O:
(1/2)d/((1-)+d/(+1))
=d/(1-2) (1)
Le point O est à (1) du point A.
Pour le rayon, on fait la différence:
(1/2)d/((1-)-d/(+1))
=d/(1-2) (2)
Le rayon est (2)
Mais après pour démontrer que ca fait une sphère, il faut démontrer que pour tout point P vérifiant r'=r, OP=(2)
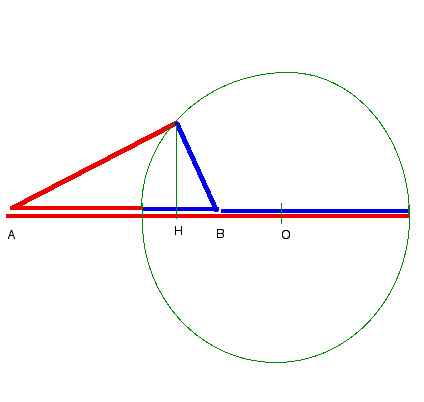
Et là??? peut-être trouver le projeté orthogonal de P sur (AB) (appelons le H), calculer la distance entre PH, calculer OH, et appliquer Pythagore dans OHP rectangle en H.
Bon courage!!!
Je complete ce que j'ai dit:
je trouve, avec les lettres précédentes:
OH=
par contre, pour la suite, ca complique beaucoup...
Merci de m'aider Eric1, mais la je ne vois pas vraiment comment tu arrives a ces resultats (j'avais prévenu, je ne suis pas doué en electrostatique).
Par exemple je ne vois pas bien comment tu as trouvé O.
Merci de m'eclairer !
Car à partir de ce que j'ai écrit, ce ne sont que des maths... l'éléctrostatique, c'était juste la question 1
Effectivement, apres ce n'est que de la géométrie, mais en fait si je comprends bien, tu as deviné qu'il y aurait 2 points P tels que r'=r sur(AB), tu a determiné leur distance respective par rapport a A et ensuite tu as cherché ou se trouverait un eventuel centre ce cercle, et son rayon (à la base rien ne nous dit que le centre du cercle est sur (AB) ).
Ensuite je comprends bien ou tu veux en venir et je devrais tomber sur la meme forme de OH que toi, merci beaucoup !
As-tu compris comment determiner le centre et le rayon
D'autres part, mon explication est incomplète, car ce n'ets pas parceque ca coupe la droite en 2 points que le rayon se situe sur (AB). Mais il aurait fallut préciser qu'il y a une symétrie, de par les longueurs, ce qui prouve que le centre de la sphère ne peut se trouver que sur (AB)
seulement, mon raisonnement pour le calcul dyu rayon est un peu erroné, car H peut se situer de part et d'autre de O..
J'ai compris pour le centre et le rayon, la je vais chercher pour le projeté de P sur (AB), je suis en MP mais en MPSI je n'ai pas pu suivre tous les cours d'electrostatique (d'ou mon retard sur cette partie du programme ...)
Ok, merci pour tes explications ! Ce que je n ai pas encore compris c est ce que tu dis sur la symetrie par les longueur qui implique que O est forcement sur (AB), est ce que je peux supposer que O est sur (AB) et ensuite montrer que l'hypothese est bonne ou alors y'a t il des arguments plus appropriés ? (j'ai deja étudié tout plein de symetries mais celle la ...)
Le problème, c'est qu'il faudrait fixer un repère pour mieux le démontrer.. Mais on a l'égalité: AP=r, BP=r
Or, si on met H, le projeté orthogonal de P sur (AB), on voit bien que cette égalité est respectée sur le cercle de centre H, et de rayon [HP] dans le plan perpendiculaire à (AB)
On a donc une symétrie cylindrique d'axe (AB), ce qui prouvera, dès qu'on aura montré que dans le plan (ABP), l'équation est un cercle, on pourra le généraliser dans l'espace à l'aide de cette symétrie pour donner une sphère...
Annuler
connectez vous