Bonjour, je n'arrive pas à comprendre le raisonnement fait sur ce genre d'exercice :

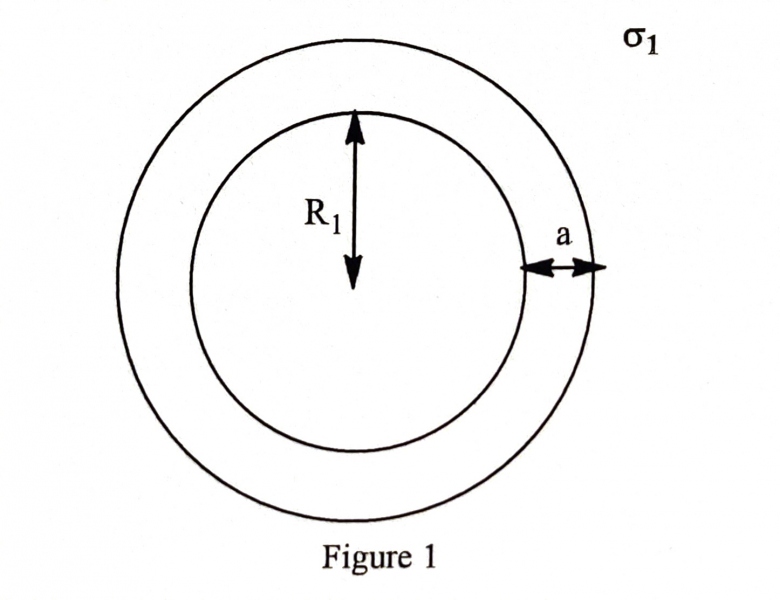
Une sphère creuse de rayon interne et porte une densité surfacique de charge sigma1<0. Cette sphère est parfaitement conductrice et son épaisseur est notée a


dans un premier temps, on me demande où se répartissent les charges au niveau de cette coquille sphérique : elles se trouvent bien sur la face externe


Ensuite, On place dans cette sphère creuse  une autre sphère pleine, concentrique, de rayon R2<R1 et portant une densité volumique p2>0.

Donc là ils veulent que j'exprime sigma1 en fonction de R2 R1 et p2



Mon problème n1  :
le corrigé me dit que "on applique le théorème de gauss en un point M à l'intérieur de la coquille, on a donc E(M)=O (en vecteur)  etc "

(le point M est placé dans la correction, au milieu de l'épaisseur a )

Donc juste avec cette phrase du corrigé, je ne comprends pas :
on me dit que la sphère creuse est conductrice donc son E interieur =O
mais dans ce cas ci, on a ajouté une nouvelle sphère pleine chargée et non conductrice je crois, au sein de la sphère précedente. Donc à mon avis, cette sphère pleine émet un champ électrique autour d'elle, et donc le point M ressentirait cette fois ci un champ.
En effet, les vecteurs du champ electrique de la sphère conductrice s'annulent, et donc en ajoutant la nouvelle sphère, de "nouveaux vecteurs" du champ electrique de la nouvelle sphère s'ajoutent par dessus de ceux de l'ancienne sphère. Donc il y a tout de même un champ non nul au point M

Donc c'est comme cela que je vois les choses, mais je ne comprends pas pourquoi on dit alors que même dans ce cas ci , E(M)=O ?




problème n2 :

Donc le corrigé poursuit en disant :
"... On a donc E(M)=O
Qint/eo     = O    (eo = epsilon)

Or la charge intérieure contenue à l'interieur de cette surface de gauss est du à la contribution de la sphère de rayon R2 chargée en volume et des charges qui apparaissent en surface au niveau de la face interne de la coquille sphérique sigma1 :
Qint = Q1+Q2
avec Q1=sigma.S    Q2=pV etcc"

Donc mon 2eme problème est que :

Plus haut, on avait dit que les charges se répartissaient bien sur la face externe et que par conséquent, la charge à l'intérieur de la surface externe est nulle (puisque conductrice)
Donc je ne comprends pas pourquoi le corrigé mentionne que la surface chargée contient les charges de la surface INTERNE ? Pourtant la coquille est chargée seulement surfaciquement et la surface la plus "éloignée" est la surface externe, et c'est sur celle ci où les chargent vont avoir tendance à se placer

Voila mes 2 problème, j'éspère que c'est clair

Merci d'avvance