Inscription / Connexion Nouveau Sujet
Electrostatique et Loi de Coulomb
Bonjour à toutes et à tous ^^ J'espère que vous allez bien.
Je prépare les concours GEI (pour intégrer une école d'ingénieur après la fac) et j'ai un problème concernant un exercice. Voici l'énoncé:
"Trois charges identiques Q se trouvent sur les sommets d'un triangles équilatéral de coté a. Calculer la valeur absolue de la force éprouvée par une des trois charges en fonction de x, la distance entre le centre du triangle et la charge"
J'ai trouvé x = a/sqrt(3) et donc a² = 3x².
Après cela j'applique la loi de Coulomb mais je suis toujours bloqué.
En effet je trouve:
F = k.(Q²/3x²)
Cette exercice est un QCM et aucunes des réponses ne correspond à ça.
J'ai le choix entre:
F = k.(Q²/x²)
F = k.(Q²/sqrt(3)x²)
F = k.(Q²/sqrt(5)x²)
F = k.(2Q²/sqrt(3)x²)
F = k.(3Q²/sqrt(3)x²)
Je dois sûrement faire une erreur bête ou alors il faut que j'applique une autre règle mais elle ne me vient pas en tête. Serait il possible de m'aiguiller sur ce problème ?
Merci à tous.
Bonsoir
As-tu fait un schéma précis représentant les forces électrostatiques exercées sur une charge par les deux autres ? Tu peux le scanner et le poster ici. Tu peux aussi expliquer ton raisonnement.
Bonsoir
Concernant le schéma je n'ai fait qu'un triangle avec une charge à chaque extrémité et un point x représentant le centre de mon triangle équilatéral. Chaque coté de mon triangle a une longueur noté a.
J'ai trouvé la valeur de x = a/sqrt(3) donc dans la loi de Coulomb il faut a² donc j'ai dit que x²=a²/3 et donc par un produit en croix je trouve a²=3x².
J'ai donc mis cette valeur dans ma loi de Coulomb et je tombe sur
F = k.Q1.Q2/d²
Les charges étant des charges identiques Q.
F = k.Q²/3x²
Après cette étape je vous avoue que je ne sais pas trop quoi faire pour arriver à une des formules présente dans la liste.
J'ai aussi essayé le fait que l'autre charge agit aussi (vu qu'on a 3 charges) donc j'ai tout multiplié par 2 mais ça ne résout toujours pas mon soucis. Je ne trouve pas de réponses présentes dans la liste donnée.
j'ai tout multiplié par 2
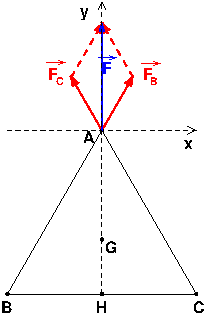
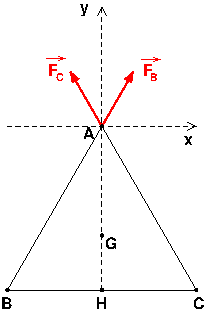
Attention : les vecteurs forces correspondant aux forces exercées par les charges en B et en C sur la charge en A . Ce sont deux vecteurs qui ne sont pas colinéaires. La norme du vecteur somme n'est donc pas le double de la norme d'un des deux vecteurs !
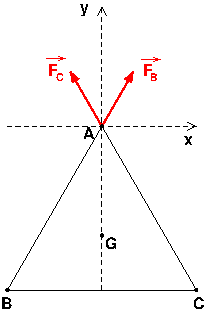
Le schéma que je te fournis, volontairement incomplet, devrait je pense t'aider. Pour trouver la somme, tu as le choix entre (au moins) trois méthodes :
1° : tracer le vecteur somme puis utiliser les propriétés géométriques du losange ;
2° : projeter la relation vectorielle sur deux axes comme tu as dû prendre l'habitude de le faire en mécanique dans l'enseignement secondaire ;
3 : Puisque le vecteur FB est colinéaire au vecteur BA, écrire le vecteur FB sous la forme :
Procéder de manière analogue sur
Bonjour
J'ai beau tout essayé rien ne marche. =(
Je ne dois toujours pas comprendre réellement quoi faire.
Deux jours bloqué sur cette question et je ne vois toujours pas le cheminement pour arriver à une des réponses présente dans la liste.
J'ai essayé vos méthodes mais n'ayant suivi aucun cours de physique dans mon parcours scolaire c'est assez complexe pour moi.
Voila ce que j'ai fait
BH + HA + CH + HA = 2HA (car BH + CH s'annulent car ils sont de même longueur et de sens opposé)
HA =(sqrt(3)/2).a
2HA = sqrt(3).a
F = k.(Q²sqrt(3)a)/ a^3
F = k.(Q²sqrt(3))/a²
On sait que a² = 3x²
F = k.(Q²sqrt(3))/3x²
Où est ce que je fais erreur ?
Comme je ne suis pas très susceptible, je vais quand même te répondre... 
Tu n'as pas commis d'erreur, juste des parenthèses mal placées dans tes formules en ligne.
Cela donne un vecteur force orienté suivant (A,y) puisque le vecteur force est colinéaire à