Inscription / Connexion Nouveau Sujet
Électrostatique, condition d’équilibre
Bonjour, voici l'énoncé qui me pose problème :
On note A, B, C et D les quatre sommets d'un carré de côté a.
On place deux autres charges q et q', respectivement en B et D.
1) Calculer la force totale appliquée sur chacune des quatre charges par les trois autres.
2) Existe-t-il des valeurs de q et q' pour lesquelles la résultante des forces subies par chacune des charges Q soit nulle ?
Ce que je propose :
1) Force totale en A= 1/4.pi.epsilon0 x Qq'/r^2 + 1/4.pi.epsilon0 x Qq/r^2 + 1/4.pi.epsilon0 x QQ/r^2
(et ainsi de suite pour chaque force, mais je crois qu'il ne faut que celle-ci pour la question 2)
Pour la question 2) je sèche car mon résultat à la 1) n'aide pas 
Ce que la correction propose :
1) Force en A= 1/4.pi.epsilon0 x Qq/a^2 + 1/4.pi.epsilon0 x (QQ/2a^2)xcos selon (i)
selon (i)
Force en A= 1/4.pi.epsilon0 x Qq'/a^2 + 1/4.pi.epsilon0 x (QQ/2a^2)xsin selon (j)
selon (j)
Encore une fois c'est une question de projection de vecteur avec la trigo qui me bloque… merci de m'aider !
Bonjour
Ton énoncé ne semble pas complet : tu ne dis rien des charges en A et en B.
Il faut commencer par faire une figure soignée en représentant les trois vecteurs forces puis projeter dans un repère bien choisi.
Tu peux scanner ton schéma et le poster ici.
L'énoncé est celui de mon sujet de TD, et malheureusement il se limite bien à ce que j'ai précisé.
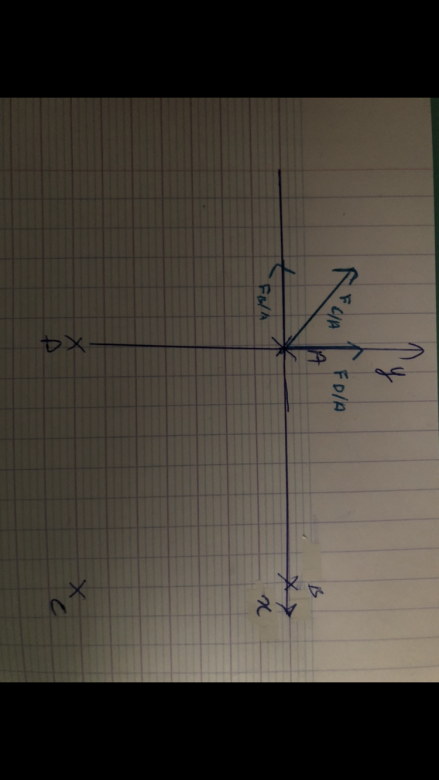
Voici le schéma que j'ai fait.
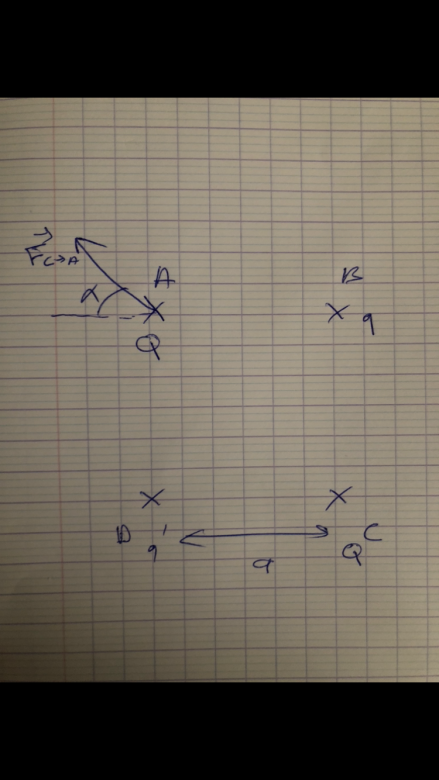
Ton schéma a le mérite de préciser les charges mais il n'est pas assez soigné pour permettre une résolution de l'exercice. Il faut y représenter les trois vecteurs forces et tracer un repère de projection d'origine A.
Tu dois bien avoir une règle quelque part...
Je sais que le vecteur force de D->A est vertical et le vecteur B->A horizontal mais j'avoue que je ne saurais pas m'y prendre pour faire un repère, c'est un peu ma difficulté.
Les trois forces sont colinéaires respectivement à AB, AC et AD. Pour les sens de ces vecteurs il faudrait en savoir plus sur ces charges en particulier leurs signes. Si rien n'est précisé à ce sujet, fais la figure avec toutes les charges positives. En cas de charges négatives, il suffira de changer les signes des projections de vecteurs. Le repère est d'origine A, l'axe des x orienté vers B et l'axe des y orienté vers le haut.
Oui. Ensuite : puisque le vecteur est colinéaire à la diagonale (CA), les angles entre ce vecteur et les deux axes valent 45°. Tu peux maintenant projeter les trois vecteurs dans le repère choisi et ainsi avoir les deux composantes du vecteur somme :
La méthode est analogue à celle que je t'ai indiquée dans l'exercice précédent.