Inscription / Connexion Nouveau Sujet
Electrostatique calcul du champ E pour une boule chargée
Bonjour
j'aurais une question concernant l'application du théorème de gauss dans le cas d'une boule chargée j'aimerais savoir pourquoi lorsque l'on intègre on intègre thêta de 0 à pi au lieu de 2 pi alors que l'on intègre phi de 0 à 2 pi .
Bonjour
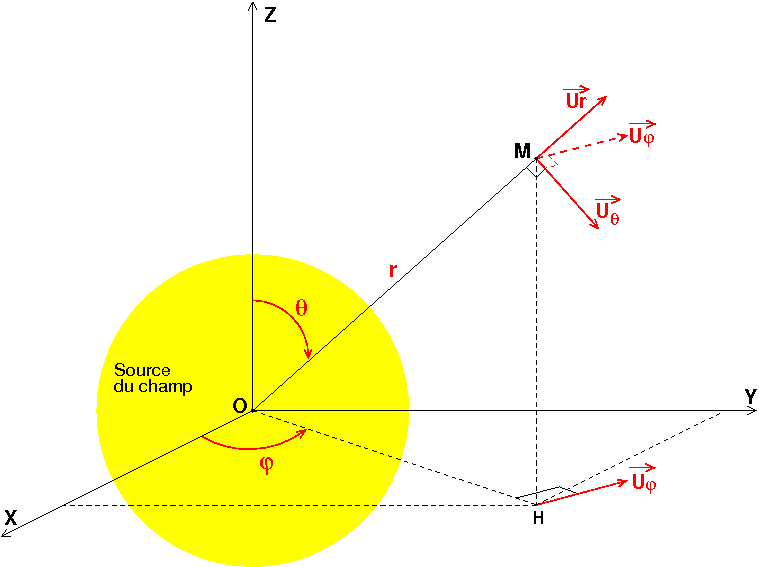
Le schéma ci-dessous t'aidera peut-être.
Imagine une petite couronne sur la sphère de rayon r=R d'épaisseur R.d et d'axe (Oz). On l'obtiens en intégrant
et d'axe (Oz). On l'obtiens en intégrant  de zéro à 2
de zéro à 2 . Pour balayer la sphère entière, il suffit de prendre l'ensemble des couronnes élémentaires comprises entre zéro et
. Pour balayer la sphère entière, il suffit de prendre l'ensemble des couronnes élémentaires comprises entre zéro et  .
.
et est ce que cela veut dire que l'on peut aussi ecrire l'inverse c'est à dire intégré phi de 0 à pi et théta de 0 à 2pi pour avoir une sphere
Il faut se méfier des éventuels problèmes de signe. Je prends le cas simple du calcul de l'aire d'une sphère de centre O et de rayon R. Compte tenu de l'expression générale d'un déplacement élémentaire en coordonnées sphériques :
L'aire d'une surface élémentaire de la sphère est :
Cela sous réserve cependant que sin( ) positif ou nul pour obtenir une aire positive.
) positif ou nul pour obtenir une aire positive.
Tu obtiens indifféremment l'aire de la sphère par :
mais :
En revanche, pour ne pas avoir le problème du sinus négatif, tu peux écrire que l'aire est le double de l'aire de l'hémisphère correspondant à y>0 :
De façon plus générale, en absence de problème de signe, il est souvent avantageux d'intégrer en  de 0 à
de 0 à  et en
et en  de 0 à 2
de 0 à 2 quand l'axe (Oz) est axe de symétrie. Il devient intéressant d'intégrer en
quand l'axe (Oz) est axe de symétrie. Il devient intéressant d'intégrer en  de 0 à 2
de 0 à 2 et en
et en  de 0 à
de 0 à  quand le plan (Oxy) est plan de symétrie.
quand le plan (Oxy) est plan de symétrie.


