Inscription / Connexion Nouveau Sujet
Electrostatique
Bonsoir,
Exercice :
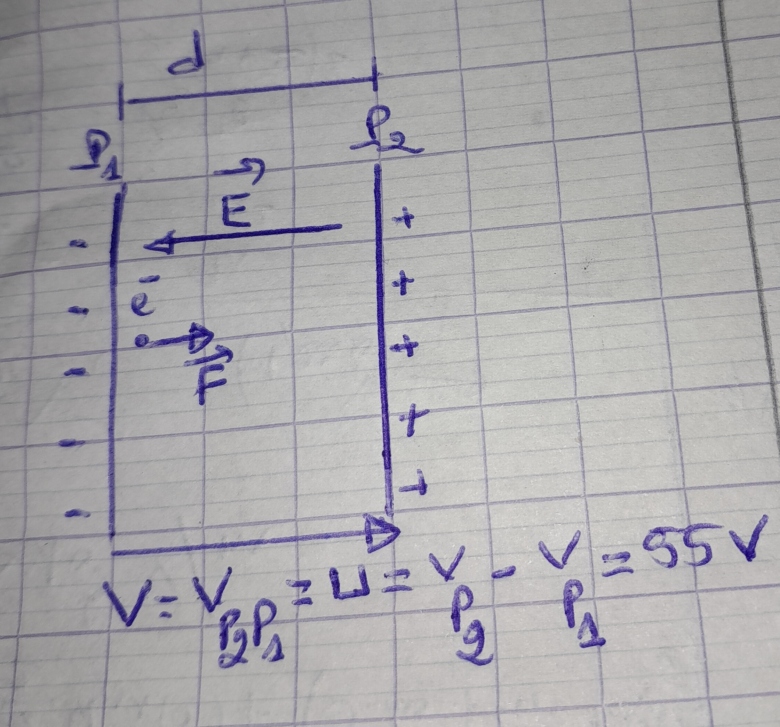
La distance entre deux plaques parallèles est de 0.050 m . un électron de masse est au repos à la surface de la plaque négative. Calculer la vitesse à laquelle il atteindra la plaque positive si on applique un potentiel de 55 V entre les plaques.
Réponse :
un schémas tout d'abord pour illustrer les s grandeurs physiques intervenants (figure ci-jointe),
première méthode : application du T.E.C
, seule force qui travaille est la force électrostatique du champ D entre les 2 plaques, le travail du poids de l'électron est nul à chaque instant car le vecteur poids est perpendiculaire à l''axe des abscisses (OX), et la vitesse initiale est nulle, donc :
ici U= V =VP2P1.
On obtient :
vP2=4.4  106V/m,
106V/m,
J'ai voulu trouver le même résultat en utilisant les concepts de conservation d'énergie :
je calcule l'énergie potentielle de l'électron :
A partir de là, je suis brouillé car si je considère l'origine des potentiels en P2 je dois mettre un signe - à la formule de Ep.e.
voilà ici mon problème.
merci de m'expliquer.
Bonsoir
La conservation de l'énergie mécanique conduit à :
0+q.VP1 =(1/2)m.V2P2 +q.VP2
Sinon il suffit de dire que le poids est totalement négligeable devant la force électrique. Il suffirait de comparer m.g à e.U pour s'en convaincre mais cela n'est pas nécessairement réclamé à chaque fois. Ton argument sur le travail du poids nul ne tient pas vraiment car, si le poids n'était pas négligeable devant la force électrique, la trajectoire ne serait pas rectiligne et horizontale.
Merci et bonsoir,
J'utilise : la conservation de l'énergie totale, ici, car on a l'énergie potentielle électrique .
Merci et bonsoir,
J'utilise : la conservation de l'énergie totale, ici, car on a l'énergie potentielle électrique .
Pardon : le quel de deux est nulle, q.v_p1 ou q.v_p2, comment son signe et pourquoi.
Merci encore.
Pardon : je continue sur le même sujet pour comparer,
Deux plaques parallèles sont séparées d'une distance de 0,0060 m. Le potentiel entre les deux plaques est 655V. Si une charge de 5, 0×10-9C se déplace d'une plaque à l'autre, quelle est la valeur de l'énergie transférée à la charge.
Ici encore je choisis : Ep.e=V×q =655×5×10-9= 3,3×10-6 J.
Donc dans les 2 cas : la charge négative ou positive Ep.e>0
Toujours brouillé dans le cas de Ep.elec= q.V
Merci de m'éclairer.
le quel de deux est nulle, q.v_p1 ou q.v_p2, comment son signe et pourquoi.
Peu importe ! Comme déjà plusieurs fois écrit : le choix de la référence de potentiel nul est totalement arbitraire : seule la différence de potentiel possède un sens physique. Je reprends ma relation du 18-03-25 à 22:29 traduisant la conservation de l'énergie mécanique entre le départ de la charge q sur P1 et son arrivée sur P2 :
On voit bien que le résultat demandé fait intervenir une différence de potentiel qui a un sens précis dans une situation physique donnée et non un potentiel qui peut être défini d'une infinité de manières possible
Il y a une forte analogie avec l'énergie potentielle de pesanteur dans le cas d'un champ de gravitation uniforme. On pose Ep=m.g.z mais le niveau zéro d'altitude est choisi de façon arbitraire, seule une variation d'altitude a un sens physique. Lors d'une chute libre avec vitesse initiale nulle d'une altitude zi à une altitude zf<zi :
Ep.elec= q.V
Cette formule n'a de sens que si tu choisis au préalable l'état de potentiel nul. Mais quel que soit ce choix, la résolution d'un problème te conduira toujours à faire intervenir une différence de potentiels qui elle, possède une valeur unique bien définie pour une situation donnée. C'est ce que j'ai montré en début de ce message. Je me répète...
Pardon : je continue sur le même sujet pour comparer,
Deux plaques parallèles sont séparées d'une distance de 0,0060 m. Le potentiel entre les deux plaques est 655V. Si une charge de 5, 0×10-9C se déplace d'une plaque à l'autre, quelle est la valeur de l'énergie transférée à la charge.
Ici encore je choisis : Ep.e=V×q =655×5×10-9= 3,3×10-6 J.
Donc dans les 2 cas : la charge négative ou positive Ep.e>0
Toujours brouillé dans le cas de Ep.elec= q.V
Merci de m'éclairer.
Bonjour,
D'accord évidemment avec tout ce qu'a écrit vanoise.
Juste quelques réflexions sur ce qui me semble une mauvaise interprétation chez bush.
" Le potentiel entre les deux plaques est 655V"
Comme souligné plusieurs fois par vanoise, tu confonds potentiel et différence de potentiel... et la plupart de tes soucis viennent de là.
Donc dans les 2 cas : la charge négative ou positive Ep.e>0
Tu penses vraiment que cela revient au même que la charge placée, au départ, (par exemple) près de la plaque négative, soit négative ou positive ?


