Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Electrostatique

Posté par
bissinyandoup 19-11-17 à 09:58

Bonjour
Je souhaite avoir de l'aide sur cet exercice s'il vous plait
On me demande de calculer le champ electrostatique au centre d'un demi cercle uniformement chargé de centre C et de rayon R
Je sais que le champ elementaire est dE=dq/4π0PC2
Or PC=R,  dq=dl  et dl=Rd
Tout calcul fait, je trouve
l=πR,   q=πR.
Mais je trouve l'expression de E bizarre. De l'aide s'il vous plait

Posté par
diracre : Electrostatique 19-11-17 à 10:21

Hello

Le champ électrostatique est une grandeur vectorielle.

Tu dois donc sommer les    d\vec{E} pour obtenir  \vec{E}

Je te recommande de faire un schéma en ayant posé un système d'axe qui utilise les symétries du système.

A toi?

Posté par
bissinyandoupre : Electrostatique 19-11-17 à 11:47

Je vois. Mais bon en fait on aura
dE=dl/4π0R2.
Comment continuer a ce niveau?

Posté par
diracre : Electrostatique 19-11-17 à 15:48

Es tu certain de "voir" tant que cela

Pour un élément dl du demi cercle situé autour d'un point M:

d\vec{E} = \frac{1}{4\pi\epsilon_0}\frac{\lambda dl}{OM^3}\vec{OM}

Et donc \vec{E} = \int_{M\in\mathcal{C}}d\vec{E} =  \frac{1}{4\pi\epsilon_0}\int_{M\in\mathcal{C}}\frac{\lambda} {OM^3}\vec{OM}dl}

"Je te recommande de faire un schéma en ayant posé un système d'axe qui utilise les symétries du système. "

Bon, le schéma finalement c'est pour moi (vois ci dessous)

Que peux tu dire de la résultante (la somme) de la composante dEy?

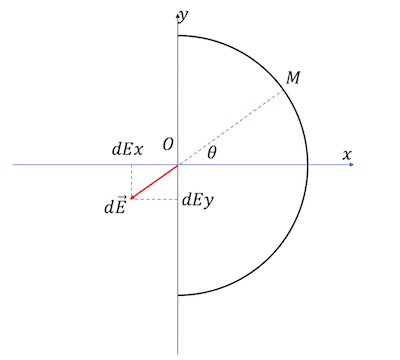
Electrostatique

Posté par
bissinyandoupre : Electrostatique 19-11-17 à 17:11

En fait Dirac j'ai du mal a te comprendre.  C'est un peu compliqué

Posté par
diracre : Electrostatique 19-11-17 à 18:14

On va y aller "étape par étape":


Etape 1: Es tu d'accord avec le fait que l'élément autour de M crée en O un champ qui vaut:

d\vec{E} = \frac{1}{4\pi\epsilon_0}\frac{\lambda dl}{OM^3}\vec{MO}

(il y avait une petite coquille dans l'expression de dE que je te donnais plus haut)

Posté par
bissinyandoupre : Electrostatique 19-11-17 à 18:23

Oui je suis d'accord

Posté par
diracre : Electrostatique 19-11-17 à 18:45



On a fait le plus dur (promis)

Tu vois que le vecteur d\vec{E} se décompose en dEx et dEy

avec:

dE_x = -\frac{1}{4\pi\epsilon_0}\frac{\lambda Rd\theta}{R^2}cos\theta

dE_x = -\frac{1}{4\pi\epsilon_0}\frac{\lambda Rd\theta}{R^2}sin\theta

Le signe - venant de la façon dont j'ai orienté les axes Ox et Oy

Est ce que arrivés là, on est toujours bons?

Posté par
diracre : Electrostatique 19-11-17 à 18:46

Pardon je voulais écrire


dE_x = -\frac{1}{4\pi\epsilon_0}\frac{\lambda Rd\theta}{R^2}cos\theta

dE_y = -\frac{1}{4\pi\epsilon_0}\frac{\lambda Rd\theta}{R^2}sin\theta

Posté par
bissinyandoupre : Electrostatique 22-11-17 à 12:38

Je crois avoir compris. Merci

Posté par
diracre : Electrostatique 22-11-17 à 13:15



Et donc? A la fin, tu trouves quoi pour E?

Résultat que je t'invite à comparer avec le cas du champ créé par un fil infini

Posté par
bissinyandoupre : Electrostatique 22-11-17 à 13:39

E=/2πR sauf erreur

Posté par
diracre : Electrostatique 22-11-17 à 14:05

Posté par
bissinyandoupre : Electrostatique 22-11-17 à 14:08


Merci

Posté par
diracre : Electrostatique 22-11-17 à 14:33

Et pour le fil infini distant de R, tu trouves quoi?   (je suis casse pieds, je sais ...)

Posté par
bissinyandoupre : Electrostatique 22-11-17 à 15:01

Eh bien, excuses moi,  mais moi je ne suis pas allé directement.
je sais que le fil est un cylindre de rayon négligeable. Donc j'ai donc calculer le champ a l'extérieur d'un cylindre en appliquant le théorème de Gauss.  Et je trouve
E=R2/2r or il y'a une relation entre et qui est = πR2. Je trouve finalement E=/2πr

Posté par
bissinyandoupre : Electrostatique 22-11-17 à 16:10

C'est bon dirac??

Posté par
diracre : Electrostatique 19-12-17 à 15:41

Suite à ton sujet de MQ , je suis allé me "remémoré" ce que nous avions déjà "fait ensemble" . Je tombe sur ce sujet sur lequel je ne t'avais pas répondu. Pas bien dirac .

Réponse: c'est bon!  

Tu as donc constaté que la résulante est la même dans le cas du 1/2 cercle de rayon R et du fil infini situé à une distance R.  


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !