Niveau licence

electrostatique

Posté par
chocohoney 01-03-11 à 10:23

Bonjour, je n'arrive pas malgrès mes nombreux essais à résoudre cet exercice, je me mélange avec tous ces vecteurs à prendre en compte !! merci de me donner la résolution détaillée car j'avoue ne pas être une lumière quand ça concerne "l'électricité" ^^'

on place 3 particules dotées respectivement de charges électriques valant +4C, -8C, -6C aux sommets d'un triangle équilatéral, dont les cotés mesurent 1,2m. déterminer la grandeur et la direction de la force nette s'exerçant sur chacune d'elle et attribuable aux 2 autres.

merci d'avance

Posté par re : electrostatique 01-03-11 à 12:48

Bonjour,
Il faut faire un schéma d'abord.
On va s'intéresser, pour le moment, aux forces sur la charge A.
$3$F_{BA}\,=\,F_{AB}\,=\,\frac{1}{4\pi\epsilon_0}\,\frac{q_A\,q_B}{d^2}$
$3$F_{CA}\,=\,F_{AC}\,=\,\frac{1}{4\pi\epsilon_0}\,\frac{q_A\,q_C}{d^2}$
Ensuite il faut faire la somme vectorielle.
$3$F_{BA}\,=\,F_{AB}\,=\,9.10^9\,\frac{4.10^{-6}\,8.10^{-6}}{1,2^2}$
$3$F_{BA}\,=\,F_{AB}\,=\,0,2\,\,N$
$3$F_{CA}\,=\,F_{AC}\,=\,9.10^9\,\frac{4.10^{-6}\,6.10^{-6}}{1,2^2}$
$3$F_{CA}\,=\,F_{AC}\,=\,0,15\,\,N$
Et la somme vectorielle ?

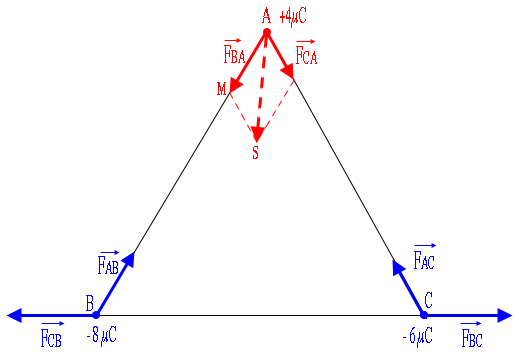
electrostatique

Posté par re : electrostatique 06-03-11 à 14:20

ah oui je vois, merci !
Mais comment s'y prend t'on pour trouver l'angle de la force ?
Par exemple, ayant trouvé pour la force résultante s'exerçant sur B 0,26N (-0,2;0,17) ?

Posté par re : electrostatique 06-03-11 à 15:47

Pour faire la somme vectorielle $\vec{F_{BA}}+\vec{F_{CA}}$ (autrement dit, trouver $\vec{AS}$ ), il faut utiliser la relation d'Al-Kashi dans le triangle AMS pour trouver $||\vec{AS}||$ .
On a : $\widehat{BMS}\,=\,\widehat{MAC}\,=\,60$ ° (angles à côtés parallèles).
L'angle qui nous intéresse pour la relation d'Al-Kashi est l'angle $\widehat{AMS}$ donc 120°

Posté par re : electrostatique 06-03-11 à 16:28

ah oui.. mais pour A, c'est un autre cas, quels sont les calculs qu'il convient de faire ?
Je ne me souviens pas de la relation d'Al-Kashi (juste de nom en fait) , qu'est ce que c'est ? Comment ça nous aide à trouver l'angle?
Merci

Posté par re : electrostatique 06-03-11 à 17:15

La relation d'Al-Kashi s'étudie en 1ère...
$AS^2\,=\,MS^2\,+\,AM^2\,-\,2\,MS\,AM\,cos(\widehat{AMS})$
Ensuite, quand on a les longueurs des trois côtés, on peut calculer l'angle qu'on veut à l'aide de la même relation ( ( $\vec{AS},\vec{AM})$ par exemple).

Posté par re : electrostatique 06-03-11 à 18:40

Donc :
$AS^2\,=\,0,15^2\,+\,0,2^2\,-\,(2\,MS\times 0,15\times 0,2\times cos(120))$
$AS^2\,=\,0,15^2\,+\,0,2^2\,-\,(2\,\times 0,15\times 0,2\times (-\,\frac{1}{2}))$
$AS\,=\,0,3\,\,\textrm{N}$
Pour préciser la position de $\vec{AS}$ , on peut calculer l'angle entre AS et AB.
$MS^2\,=\,AM^2\,+\,AS^2\,-\,2\,AM\,AS\,cos(AB,AS)$
$cos(AB,AS)\,=\,\frac{AM^2\,+\,AS^2\,-\,MS^2}{2\,AM\,AS}$
$(AB,AS)\,=\,26$ °

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

electrostatique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique