Inscription / Connexion Nouveau Sujet
Electronique ( ampli)
Bonjour à tous voila j'ai un soucis je vous le décris.
je dois exprimer vs/vs':
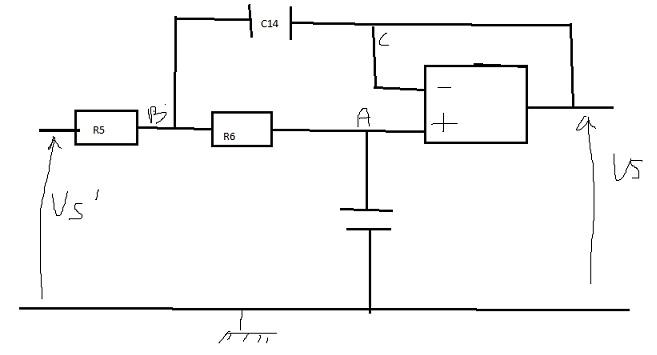
donc moi j'ai fait : milman en B :
VB =
et mais moi après je veux appliquer la linéarité V+=V- mais je trouve Vc=Vb=Vs ..... ( lorsque j'applique milman au point c !
merci d'avance ! 
Bonjour,
Il faut effectivement calculer VB avec Millman (c'est le plus simple).
VB est exprimé en fonction de v+, Vs, Ve.
Ensuite il faut exprimer VB en fonction de v+ par l'intermédiaire du pont diviseur R6 et le condensateur qui va à la masse.
On remplace VB dans l'expression précédente et on en déduit v+.
On a v- = Vs.
Il ne reste plus qu'à faire v+ = v- et on trouve Vs / Ve.
Ce circuit est un filtre passe-bas de Sallen-Kay du 2ème ordre.
Je développerai le calcul si besoin est.
Désolé de la réponse tardive !
Donc moi j'ai trouver en fesant comme tu as dis : Vb=(1+jR6Cw)V+
je remplace Vb et ensuite V+=V- =Vs je remplace et je trouve
Donc je sais pas si c'est bon déja si tu à le courage de vérifier ? 
ensuite il me demande de mettre sous la forme
c'est la que je me rend compte que mon truc est un peu louche non ? 

Pas de problème pour la réponse tardive... C'est ton exo, tu réponds quand tu veux 
Je vais vérifier ton résultat mais les notations sont désagréables : V's, C14.
Dans un but de simplification, je vais peut-être modifier les noms qui ne me plaisent pas.
Vb=(1+jR6Cw)V+ ==> OK
Ce n'est pas homogène !
Les termes du dénominateur sont sans dimension (1 est sans dimension à moins que 1 soit faux).
==> sans dimension
==> dimension =

==> dimension =

Je trouve :
Et là, c'est homogène...
En posant :
On peut écrire :
Lorsque je met en facteur ce que j'ai fait je trouve pareille que toi sauf le W qui n'est pas au Carré moi  ! va faloire que je trouve ou esc ce qu'il est parti celui la ! merci en tout cas
! va faloire que je trouve ou esc ce qu'il est parti celui la ! merci en tout cas 



