Inscription / Connexion Nouveau Sujet
Electronique
Bonsoir voila j'aurai besoin d'un peu d'aide dans un exercice de cours d'électronique. Je vous remercie par avance.
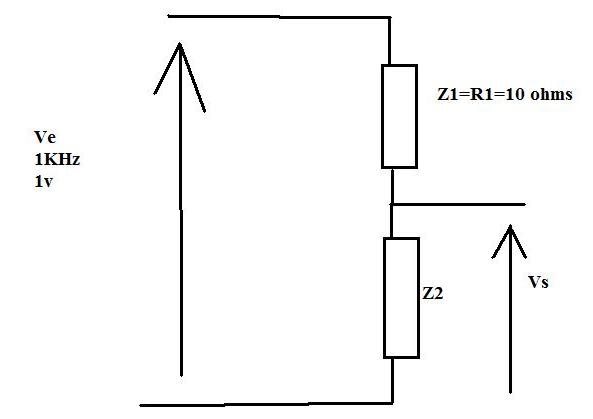
On considère le circuit suivant ( pièce jointe)
On a un gain Gv=Vs/Ve =-0.1
On doit déterminer Z2.
A la vu du moins devant le gain on sait qu'il y a un déphasage de  . On dit alors que Z2 est un condensateur car celle-ci déphase de -
. On dit alors que Z2 est un condensateur car celle-ci déphase de - /2.
/2.
On en conclut alors que l'hypothèse fait en Z1 est fausse ce ne peut être une résistance.
Je penser alors que l'impédance 1 est une bobine car du coup on aurai un déphasage de  alors du fait du condensateur et de la bobine.
alors du fait du condensateur et de la bobine.
Voici comment on nous a exposer le problème mais je n'avance pas.
Je vous remercie
j'appliquerais la loi du pont diviseur de tension
Vs = Ve * Z2 / (Z1+Z2)
On veut Vs / Ve = -0.1 d'où z2 /(z1+z2) = -0.1
essaie avec Z2 = jwL et Z1 = 1/(jwC)
Si Z1 était vraiment une résistance pure comme indiqué sur le schéma, et que Vs/Ve est bien négatif, alors, il y aurait un os.
On trouverait avec de telles conditions que Z2 est une résistance négative (ce qui est impossible, du moins avec des composants passifs).

Bonjour ,je vous remercie pour vos réponses.
Efpe j'ai calculer ce que vous me demandez et je n'arrive pas à aboutir à -0.1. j'ai:
z2/(z1+z2)=[(jwl)(jcw)]/[(jwl)(jcw)+1] que dois je faire du coup?
J-P en effet Z1 n'est pas une résistance notre professeur nous a dit dans l'énoncé que c'était une résistance mais au final il a conclut que l'hypothèse était fausse c'est pour cela que je dois déterminer Z1 et Z2.
Il est tout aussi possible que z1 soit capacitif et z2 inductif que le contraire.
Si Z1 est capacitif et z2 inductif :
Z1 = 1/(jwC)
z2 = jwL
|z1| = 10 ohms -- < 1/(wC) = 10
C = 1/(10w) = 1/(10 * 2.Pi*1000) = 15,9.10^-6 F
z1 + z2 = 1/(jwC) + jwL = (1 - w²LC)/(jwC)
i = ve/(z1+z2)
i = ve.jwC/(1-w²LC)
Vs = z2.t
Vs = jwL.ve.jwC/(1-w²LC)
vs/ve = -w²LC/(1-w²LC)
vs/ve = -0,1 ---> -w²LC/(1-w²LC) = -0,1
w²LC = 0,1.(1-w²LC)
1,1.w²LC = 0,1
w²LC = 0,1/1,1 = 0,0909
wC.wL = 0,0909
0,1.wL = 0,0909
wL = 0,909
L = 0,909.(2.Pi*1000) = 1,44.10^-4 H
-----
Autrement :
z1 et z2 sont en opposition --> z2 = -k.z1 et 0 < k < 1 et de plus |z2/(z1 + z2)| = 0,1
|-k.z1/(z1 - k.z1)| = 0,1
|-k/(1 - k)| = 0,1
k/(1-k) = 0,1
k = 0,1 - 0,1k
k = 0,1/1,1 = 0,0909
|z1| = 10 ohms
|z2| = 0,0909 * 10 = 0,909 ohms
|z1| = 1/(wC) = 1/(2*Pi*1000*C) = 10 --> C = 15,9.10^-6 F
|z2| = wL = 2*Pi*1000*L = 0,909 ---> L = 1,45.10^-4 H
-----
On peut recommencer avec z2 capacitif et z1 inductif, cela doit aussi fonctionner.
-----
Sauf distraction. 
je ne comprends pas pourquoi au début on trouve C=1/10w=1/(10*2pi*100) pourquoi w=2pi*1000
De plus d'ou sort Vs= Z2t
Je vous remercie pour l'explication par avance
w = 2Pi.f et f est imposé à 1 kHz (c'est indiqué sur le schéma).
---> w = 2.Pi*1000 = (2000 Pi) rad/s
L'impédance complexe d'un condensateur est Z1 = 1/(jwC)
Son module est donc |Z1| = 1/(wC) et il est imposé égal à 10 ohms sur le schéma.
-->
|Z1| = 1/(wC)
10 = 1/(2000.Pi.C)
C = 1/(20000.Pi) = 15,9.10^-6 F
-----
Et à la place de Vs = z2.t, il faut lire Vs = z2.i
Cela aurait du te sauter aux yeux en lisant la ligne qui suivait.
-----
Sauf distraction.