Inscription / Connexion Nouveau Sujet
Electromagnetisme
Bonsoir !
S'il vous plait j'aimerais avoir de l'aide sur cet exercice.
1)Un cône découpe sur deux sphère, de même centre O et de rayons R1 et R2 (R1<R2), deux calottes (S1) et (S2). Le volume délimité par (S1), S2) et le cône est uniformément chargé avec la densité volumique positive.
positive.
2) calculer la charge totale Q portée par le volume considéré et déterminer la force électrostatique F qu'elle exerce sur une charge ponctuelle q0 positive placé en O
3) comparer cette force a celle exercé en q0 placée en O par deux sphères de rayons R1 et R2.
Comme charge totale, j'ai trouvé
Q=4π (R23-R13)/3 et
(R23-R13)/3 et
F=q0 (R23-R13)/3
(R23-R13)/3 0r2.
0r2.
Mais la dernière question me dépasse. Je ne la comprend pas
Bonsoir
Je ne sais pas comment travaille ton professeur mais, déjà une bonne vingtaine d'années, la grande majorité des cours commence par l'étude systématique des propriétés des plans de symétrie de la source. On démontre que, si la source possède un plan de symétrie passant par le point M où on calcule le vecteur champ, ce vecteur champ en M appartient à ce plan. S'il existe deux plans de symétrie passant par M, le vecteur champ en M à pour direction la droite commune aux deux plans de symétrie (cela aurait été bien utile pour étudier le vecteur champ créé par un demi cerceau ! ).
).
S'il existe trois plans ou plus de symétrie passant par le point M, le vecteur champ ne pouvant appartenir à la fois à tous ces plans est nécessairement le vecteur nul !
Bref : sans aucun calcul, tu peux affirmer que le champ créé en son centre par une sphère chargée uniformément en surface (ou en volume d'ailleurs) est le vecteur nul.
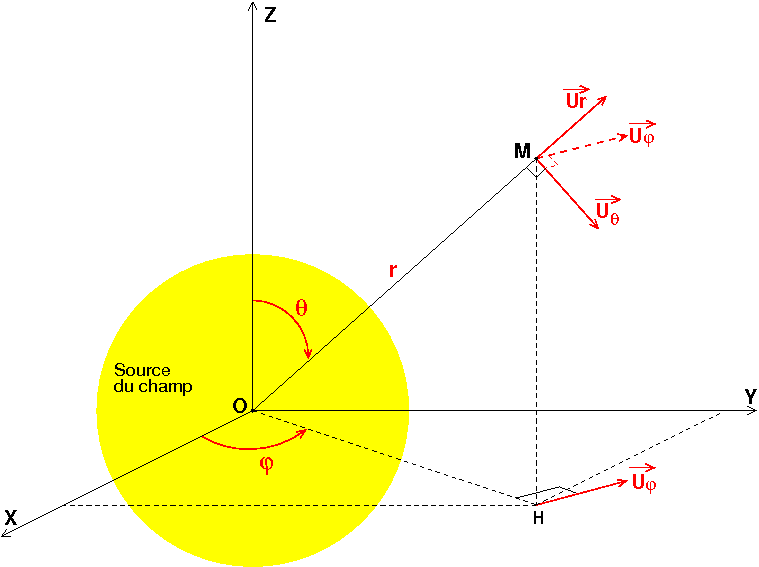
Tu pourras, si cela t'intéresse, trouver la démonstration ici ; le raisonnement sur les invariances est aussi intéressant dans l'éventualité d'une utilisation du théorème de Gauss
![]()
Laisse tomber pour l'instant la partie concernant le magnétisme
Merci Vanoise mais le problème est qu'on ne me demande pas le champ électrique. En fait mon problème se repose sur la troisième question de l'exercice. Comment calculer cette force.
Je reviens sur les questions 1 et 2.
Je n'ai pas pris le temps de vérifier ton calcul concernant la charge Q.
Concernant la force : que vient faire ici ce "r" ? Je crois qu'il faut en fait déterminer le vecteur champ E créé en O par la répartition volumique de charge de charge totale Q puis écrire :
F=qo.E
Petite question : la notion d'angle solide : cela te dit quelque chose ?
Peut-tu expliquer comment tu as obtenu l'expression de Q ?
Je suppose le cône de même sommet O que les deux sphères : ai-je raison ?
Comment est défini ce cône : valeur du demi angle au sommet ?
Un scan du schéma serait le bienvenu ; L'expression de Q que tu obtiens suppose une densité volumique de charge uniforme dans tout l'espace entre les deux sphères. D'après ce que j'ai compris (mais sans schéma, je me trompe peut-être), il s'agit de la distribution de charge de la question 3. Pour les questions 1 et 2 : les charges sont dans la partie commune à cet espace et à l'intérieur d'un cône de sommet O...
En coordonnées sphériques le volume élémentaire s'écrit (voit schéma pour fixer les conventions, ne te préoccupe pas de la sphère jaune et des mots "sources du champ") :
Le volume où sont localisées les charges est :
Cela devrait t'aider...
 o : demi angle au sommet du cône.
o : demi angle au sommet du cône.
Excuses moi d'apres ton schéma je veux dire ton esquisse. Le demi angle te donne combien ? Moi j'ai π/4
Le demi angle au sommet que j'ai noté  o devrait être fourni par l'énoncé ! Sinon, le problème ne peut être résolu !
o devrait être fourni par l'énoncé ! Sinon, le problème ne peut être résolu !
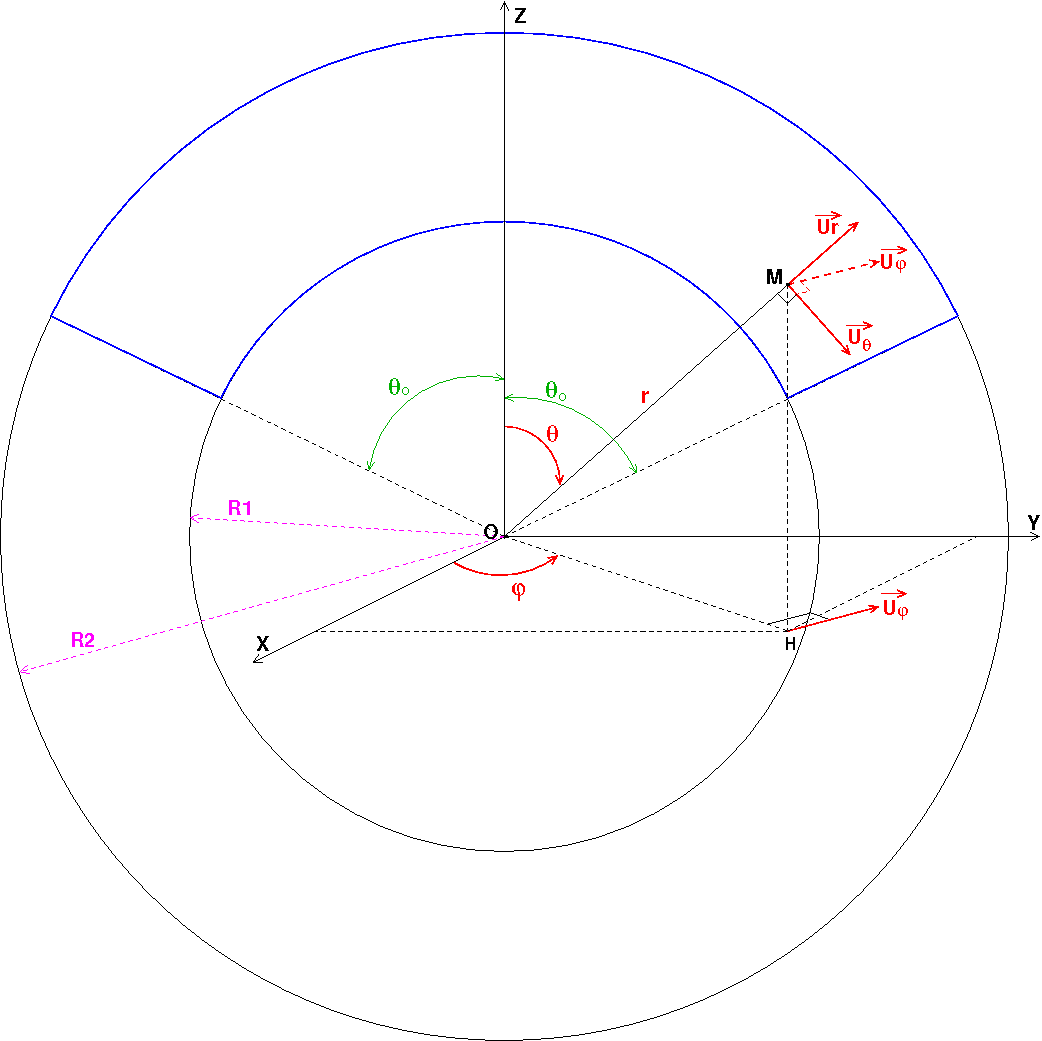
Voici un schéma un peu plus précis. Si j'ai bien deviné l'énoncé, les charges sont localisées dans l'espace délimité en bleu. Evidemment, il faut imaginer le problème en 3D en imaginant que la figure que je fournis est invariante par rotation autour de l'axe (O,z).
Finalement : on peut se passer de la notion d'angle solide.
Une fois trouvé l'expression du volume V en fonction de R1, R2 et  o, tu obtiens immédiatement Q puisque la densité volumique de charge est constante.
o, tu obtiens immédiatement Q puisque la densité volumique de charge est constante.
Pour la détermination de l'expression du vecteur champ E créé en O par la distribution de charge, n'oublie pas de commencer par déterminer les plans de symétrie de cette distribution de façon à obtenir sans calcul la direction du vecteur champ... Mon premier message est vraiment important...
Mais vanoise pourquoi calculer le champ électrique avant de calculer la force F alors qu'on peut appliquer la formule
F=q0Q/4π r2 r étant la distance séparant les deux charge. Q étant la charge totale calculé plus haut
r2 r étant la distance séparant les deux charge. Q étant la charge totale calculé plus haut
Parce pour être franc je ne sais quelle méthode pourra me donner le champ au centre. Du moi sauf si je considère que le point O est a l'extérieur de la distribution volumique considéré.
La formule que tu évoques :
donne la force d'interaction entre deux charges ponctuelles distantes de r. Ce n'est pas la situation étudiée ici ! Il faut bien revoir ton cours et les conditions de validité de chaque formule !
Si j'ai bien compris l'énoncé qui n'est pas très clair: soit le volume à l'intérieur du cône ; soit d'autre part le volume entre les deux sphères ; le volume où sont localisées les charges créant le champ en O, est l'intersection de ces deux volumes . Pour visualiser ce volume sur la figure, il faut considérer la surface délimitée en bleu et imaginer le volume engendrée par la rotation de cette surface autour de l'axe (O,z). Le point O où il faut déterminer le vecteur champ est à l'extérieur du volume contenant les charges créant ce champ...
En fait Vanoise ça devient plus compliqué que ce que je pensais. Si j'ai bien compris ce que tu dis, le volume ou sont logé les charges est l'intersection entre le volume du cône que je note V' et le volume entre les deux sphère que je note V''
Or
V''=4π(R23-R13)/3 et
V'=π(R22-R12)h. C'est exacte?
h étant la hauteur du cône bien évidemment. Mais ici on a deux sphères. La valeur de h m'est difficile a trouver.
La valeur de h m'est difficile a trouver.
Et oui ! Si je comprends bien l'énoncé (pas très clair), il faut supposer la hauteur h du cylindre nettement supérieure à R2. Ainsi, la surface supérieure limitant le volume occupé par les charges n'est pas la base du cône mais la sphère de rayon R2. Regarde encore le schéma que je te fournis et en particulier la partie délimitée en bleu. Pour une meilleure compréhension, je te joins une nouvelle version débarrassée de tout ce qui concerne les coordonnées sphériques. Ensuite, imagine que la figure tourne autour de l'axe (Oz)...
Une fois visualisée la situation, tu pourras faire le calcul du volume occupé par les charges en utilisant le contenu de mon message du 24-11-17 à 20:35 ; tu obtiendras ainsi l'expression de Q ; il te resteras à exprimer ensuite le vecteur champ en O créé par ces charges...
Tout calcul bien fait(sauf erreur) me donne
V=2π(R23-R13)(1-cos 0)/3
0)/3
Q=2π (R23-R13)(1-cos
(R23-R13)(1-cos 0)/3
0)/3
Pour calculer E je décide d'appliquer le théorème de gauss. Mais un problème surgit
le choix de la surface de gauss
Comment choisir la surface de Gauss respectant les propriétés suivante :
-elle passe pas le point ou on veux calculer le champ (O)
-le champ doit être colinéaire a la surface
D'accord avec ton expression de Q. Tu peux remarquer que le cas particulier o=
o= rad conduit au résultat que tu as fourni dans ton premier message : les charges occupent alors tout l'espace entre les deux sphères.
rad conduit au résultat que tu as fourni dans ton premier message : les charges occupent alors tout l'espace entre les deux sphères.
Pour le vecteur champ :
Il est indispensable de commencer par t'intéresser aux éventuels plans de symétrie contenant le point O où il faut déterminer le vecteur champ. On voit d'emblée que tout plan contenant l'axe (Oz) est plan de symétrie de la distribution de charges. Pour appartenir à la fois à tous ces plans, le vecteur champ doit être colinéaire à (Oz). Compte tenu du signe de  , on peut poser :
, on peut poser :
où E désigne la norme du vecteur champ.
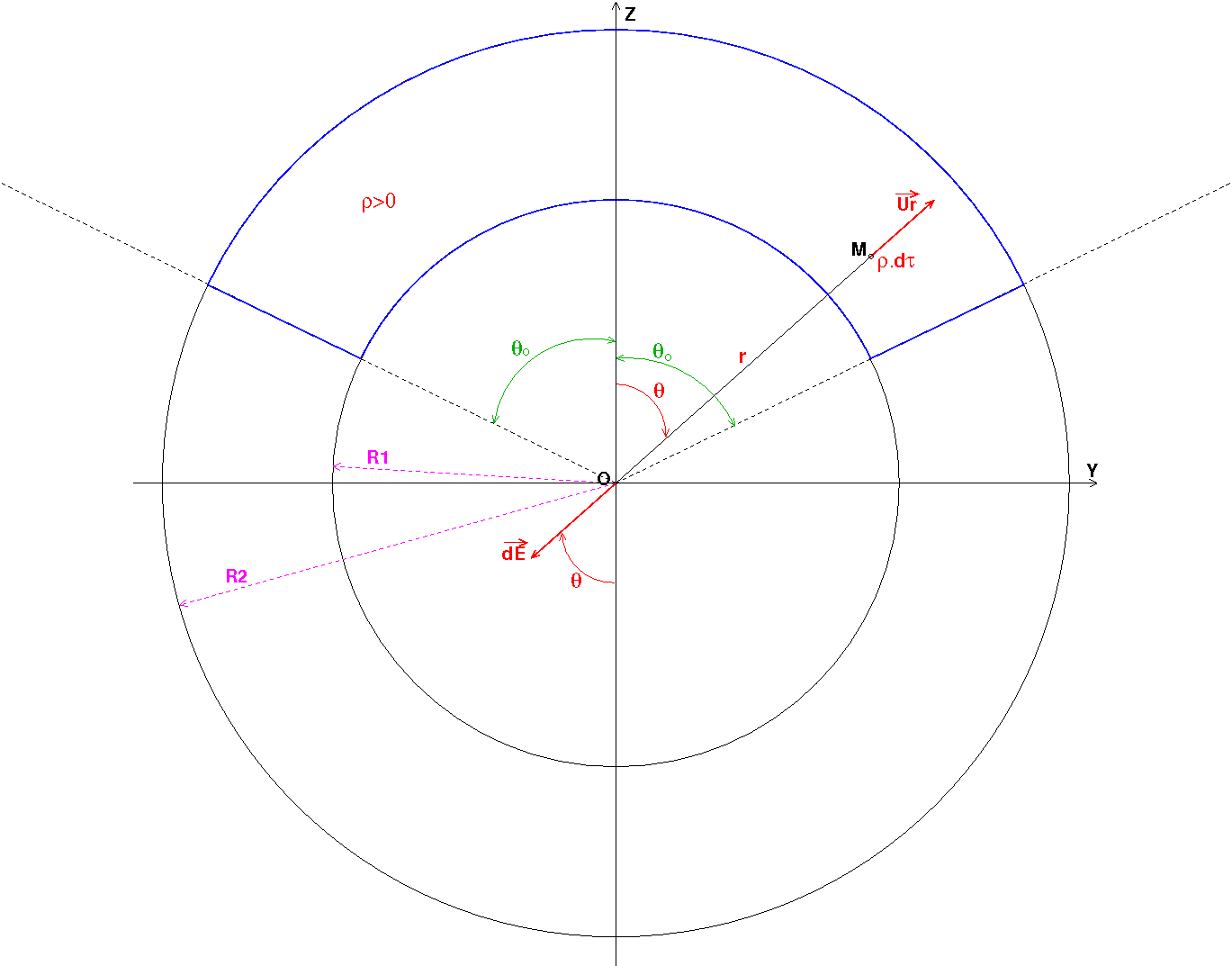
Pour envisager l'usage du théorème de Gauss, il est indispensable d'étudier les invariances de la source (revois le document que je t'ai fourni). Il n'y en a aucune : il est impossible de trouver une surface fermée passant par O permettant de calculer simplement le flux du vecteur champ. Le théorème de Gauss ne convient pas ! On revient donc à la classique méthode de découpage. Voir dernière figure fournie : la charge élémentaire  .d
.d centrée en M crée un champ élémentaire de vecteur en O :
centrée en M crée un champ élémentaire de vecteur en O :
Compte tenu de la direction du vecteur champ, seules les composantes de ces vecteurs élémentaire suivant (Oz) sont à prendre en compte, les autres s'annulent entre elles. Pour obtenir E, il faut donc faire la somme des quantités élémentaires :
Tu n'as plus qu'à intégrer entre les mêmes bornes que pour le calcul de Q... Tu devrais vérifier que le cas particulier  o=
o= rad correspond à un vecteur champ égal au vecteur nul comme expliqué dans mon tout premier message (toujours les fameux plans de symétrie !)
rad correspond à un vecteur champ égal au vecteur nul comme expliqué dans mon tout premier message (toujours les fameux plans de symétrie !)

 =dS/r2
=dS/r2