Inscription / Connexion Nouveau Sujet
Electromagnétisme
Bonsoir,
J'ai un exercice d'électromagnétisme, dont je n'arrive pas à exprimer R dans la base  ,
, ,
, et à intégrer puis je ne comprend pas la question 2.
et à intégrer puis je ne comprend pas la question 2.
Voici l'énoncé:
Une spire circulaire de centre O, de rayon R et d'axe (x'Ox) est uniformément électrisé avec la charge linéique  .
.
1) Calculer le champ électrique en un point M de l'axe.
Je sais que dE=(1/4
 o)(
o)( dl/r3)*r(vecteur)
dl/r3)*r(vecteur)
et dl=Rd , r=
, r= R2+x2
R2+x2
Je dois exprimer R dans la base  ,
, ,
,
 orienté suivant x,
orienté suivant x,  vers le fond et
vers le fond et  vers le haut.
vers le haut.
2) Calculer directement le potentiel V en ce même point. Retrouver l'expression du champ électrique.
Bonjour mac9,
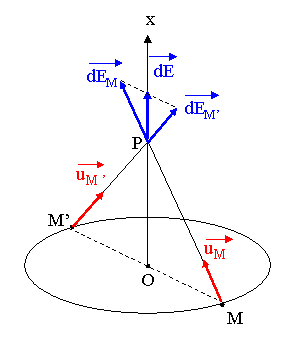
ce n'est pas un un probleme bien difficile... regarde la figure ci-dessous :
Je prends un point M sur le pourtour de l'anneau, et un petit element dl de longueur place en M. Cet element porte la charge dq =  .dl. Le champ dEM (je mets en gras pour les vecteurs) cree au point P par cette charge est dEM = (1/4
.dl. Le champ dEM (je mets en gras pour les vecteurs) cree au point P par cette charge est dEM = (1/4
 0).
0). dl.uM/MP2, avec OM = R, OP = x et MP = (x2 + R2)1/2.
dl.uM/MP2, avec OM = R, OP = x et MP = (x2 + R2)1/2.
On envisage le point M' symetrique de M par rapport au centre O de l'anneau. M' cree en P le champ dE'M et tu peux voir que ces deux champs elementaires ont sur le plan horizontal des projections qui se compensent, et sur l'axe vertical Ox des projections qui s'additionnent. Cela veut dire que le champ resultat est porte par l'axe Ox (un raisonnement s'appuyant sur les xymetries conduit au meme resultat0.
Donc il faut projeter le vecteur dEM sur l'axe Ox avant de faire l'integration, soit dE = (1/4
 0).
0). dl.cos
dl.cos .uM/MP2, ou
.uM/MP2, ou  est l'angle entre Ox et MP, soit cos
est l'angle entre Ox et MP, soit cos = z/MP.
= z/MP.
On en deduit facilement dE = 2 z.dl/4
z.dl/4
 /MP30, ce qui en additionnant le long du contour de l'anneau (ca revient a additionner dl, soit 2
/MP30, ce qui en additionnant le long du contour de l'anneau (ca revient a additionner dl, soit 2 R) donne E =
R) donne E =  R.z/2
R.z/2 0/MP3. Est-ce OK ?
0/MP3. Est-ce OK ?
Maintenant pour le potentiel : plus facile car il n'y a pas de projections a faire (le potentiel est un scalaire, pas un vecteur).
dV =  .dl/4
.dl/4
 0MP, ce qui apres integration (on remplace dl par 2
0MP, ce qui apres integration (on remplace dl par 2 R) donne V =
R) donne V =  R/(2
R/(2 0MP) = (
0MP) = ( R/2
R/2 0).(R2 + x2)(-1/2).
0).(R2 + x2)(-1/2).
La relation entre le champ electrique et le potentiel V est vectoriellement E = -grad.V, ce qui ici donne Ex = -dV/dx. Il ne te reste donc plus qu'a calculer la derivee de V(x) parrapport a x, d'y mettre unsigne - et de verifierquetu retrouve bien la norme du champ.
A bientot, prbebo.