Inscription / Connexion Nouveau Sujet
Electrocinétique, résonance pour un circuit RLC parallèle
Bonjour,
Dans mon exercice, il y a un circuit RLC parallèle avec un générateur de courant, une bobine, une résistance et un condensateur, avec une tension v(t) qui est tout à droite du schéma (sur toute sa hauteur).
La donnée est que le courant fournit est un courant sinusoïdal de la forme i(t)=Imcos( t)
t)
La question sur laquelle je bloque est celle où il faut déterminer l'amplitude Um et la phase  de la tension v(t), en faisant apparaître la pulsation propre
de la tension v(t), en faisant apparaître la pulsation propre  0 et la facteur de qualité Q du circuit.
0 et la facteur de qualité Q du circuit.
Déjà, je ne sais pas s'il faut écrire en représentation temporelle ou complexe.
J'ai commencé en représentation temporelle, et j'ai essayé d'écrire l'équation différencielle du circuit, en partant avec la loi des mailles :
i=i1+i2+i3
Je tombe sur :
(d²i/dt) + (1/RC)(di/dt) + (1/LC)i1 = (Imcos( t))/(LC)
t))/(LC)
où 1/LC est  0² et 1/RC est
0² et 1/RC est  0/Q.
0/Q.
Ensuite, c'est là que je suis bloquée, parce que je ne sais pas comment en déduire l'amplitude et la phase.
Merci d'avance si vous savez comment faire.
Bonsoir : j'ai un peu de mal à visualiser ton circuit, précisemment ton v(t)
il y a un générateur qui délivre une tension, est ce déjà une donnée que l'on peut utiliser ?
Ensuite le le circuit RLC, qui j'imagine est constitué d'un R, L et C qui sont en série, cet ensemble est en parallèle avec un générateur?
car si chacun des constituants est en parallèle avec l'autre alors V(t) = tension du générateur...
Peux-tu faire un schéma STP ?
Voilà un schéma.
Mais c'est bien un générateur de courant (ou de tension) ?
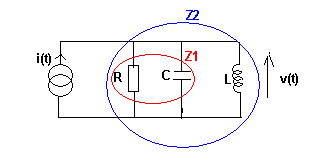
Z1 : R // C:
Z1 = (R/(jwC))/(R + 1/(jwC))
Z1 = R/(1+jwRC)
Z2: R // C // L
Z2: Z1 // L
Z2 = [jwLR/(1+jwRC)]/[jwL + R/(1+jwRC) ]
Z2 = jwLR/(R-w²LRC + jwL)
v(t) = Z2.i(t)
v(t) = [jwLR/(R-w²LRC + jwL)] * Im.cos(wt)
|Z2| = wLR/(racine((R-w²LRC)²+w²L²))
|v| = Im * wLR/(racine((R-w²LRC)²+w²L²))
|v| = Im * wLR/(racine(R²(1- w²/wo²)²+w²L²))
Phi = arg(Z2) = Pi/2 - arctg(wL/(R-w²LRC))
Phi = Pi/2 - arctg(wL/(R(1- w²/wo²)))
Tu peux introduire Q en triturant mes équations, mais attention, li faut prendre la bonne formule pour le Q.
Ne pas confondre les expresssions de Q du circuit série et du circuits // (et je pense que c'est ce que tu as fait).
Je n'ai rien relu, et donc tous mes calculs sont à vérifier.

Bonjour,
Merci beaucoup pour votre aide !
Mais je bloque à une autre question, où il demande de calculer numériquement "oméga" 1 et 2, c'est pour détermnier la bande passante.
On connait les valeurs numériques de R, L, C et Im mais je ne sais pas quelle formule utiliser.
Merci encore.
A la résonnance, w²LC = 1, soit w=wo --> |v| = Im * wLR/(racine(R²(1- w²/wo²)²+w²L²))
|v|max = Im * wLR/(racine(w²L²)) = R * Im
La bande passande est en général définie pour |v|(w) = |v|max/racine(2)
--> Im * wLR/(racine(R²(1- w²/wo²)²+w²L²)) = R * Im/racine(2)
wL/(racine(R²(1- w²/wo²)²+w²L²)) = 1/racine(2)
racine(2). wL = racine(R²(1- w²/wo²)²+w²L²)
2.w²L² = R²(1- w²/wo²)²+w²L²
w²L² = R²(1- w²/wo²)²
wL = +/- R(1- w²/wo²)
a)
wL = R(1- w²LC)
w²RLC + wL - R = 0 -->
w1 = [-L + racine(L² + 4R²LC)]/(2RLC)
b)
wL = - R(1- w²LC)
w²LRC - wL - R = 0
w2 = [L + racine(L² + 4R²LC)]/(2LRC)
La bande passante s'étend de w1 = [-L + racine(L² + 4R²LC)]/(2RLC) à w2 = [L + racine(L² + 4R²LC)]/(2LRC)
Elle vaut w2-w1 = 1/RC et est centrée sur w = (w1+w2)/2 = racine(L² + 4R²LC)]/(2RLC)
Ceci donné en pulsation, si on veut la bande passante en fréquence, il suffit de diviser par 2Pi
Bande passante de 1/(2Pi.RC) Hz centrée sur la fréquence racine(L² + 4R²LC)]/(4.Pi.RLC) Hz
-----
Sauf distraction (calculs à vérifier). 


