Bonjour,

2(R/4) = R/2

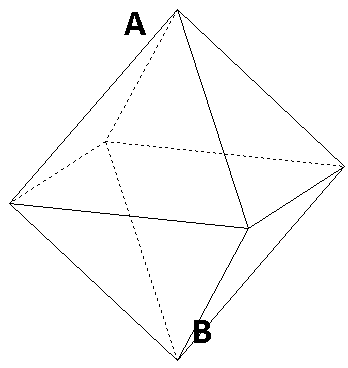
Bonjour

Je voudrais une méthode , je connaîs le résultat je n'arrive pas à le trouver .

Comment avez-vous fait ?

Merci

Quel est le plan "d'antisymétrie" entre A et B ?

le plan d'antisymétrie est EFGH (la base de l'octaèdre)

petite réponse?

Salut, j'étudie en ce moment l'électrocinétique aussi.. je pense qu'il faut que t'utilises le fait que 2 points symétriques ont le même potentiel (note les points, ce sera plus facile)
ensuite c'est tout simple, ces deux points qui ont un même potentiel, tu les relie par un fil.
Ensuite t'utilises les équivalences.

Oui c'est ça, au final tu te retrouves avec une résistance équivalente (et ce sera égal à un nombre de petit r)

où sont les petits r ?

j'arrive pas à voir

relis ton énoncé..

"Sachant que chaque branche possède la même résistance r.."
tu cherche les résistances équivalentes

chaque branche a r
Mais j'ai quelles branches là ? j'enlève la base ?

Je te donne un exemple:

Soient C,D,E,F les points de la base carrée (C,D devant, E,F, derrière)

tu peux considérer que C est le symétrique de E par rapport à (AB)
que D est le symétrique de (AB) par rapport à F

Donc VC= VE
et VD=VF

qu'est-ce que j'écris sur mon dessin parce que je vois pas

Non, en tout tu as 12 r (12 branches ici)
notes les noeuds

tous les noeuds ?

peux-tu me faire un petit dessin ?

tu sais ce que c'est un noeud quand même?

moi j'ai 6 noeuds

oui je crois jen ai 6 et toi ?

tu la vois la base carrée? et bien tu la nomme CDEF (comme je te l'ai dit précédemment)

refais le dessin, avec la base carrée CDEF et les résistances r, tu verras, c'est beaucoup plus simple

lol, oui
(bon un noeud c'est un un point qui relie au moins 2 fil)
donc là t'en a 6
mais t'en a 4 qui ne sont pas nommés, bon tu les nomme CDEF

j'ai 9r

1 sur : AC,AD,AE,CB CD DB BE DE AF FE 10 EN FAIT

Excuse-moi, j'ai dû partir.

Non, il y en a 12:

AC,AD,AF,AE
BC,BD,BF,BE
CD,DF,FE,EC

En voici un exemple

Ok j'ai oublié de déssiner 2 arrêtes

Bon, c'est juste pour t'aider à mieux visualiser.

Ensuite, t'auras des résistances montés en dérivation, tu fais plusieurs équivalences, et t'obtient Reqtotal

c'est bon je pense avoir compris

pourquoi as-tu fais 2 traits pour c et E ?

Parce que C et E sont reliés à B.

(j'ai pas fais la suite)

d'accord

pas grave s'il n'y a pas la suite je pense avoir tout à fait compris ! ^^

Merci beaucoup pour avoir pris le temps de m'expliquer tout ça !^^

Bonne soirée

question : la branche AF  et FC sont bien en dérivation ?

Euh à vrai dire, je ne pourrais te le dire (j'ai pas de papier sur moi là), mais en gros, suis attentivement le schéma, et ça devrait aller

A la fin, t'as Req= xr

De rien, entre MathsSup on s'soutient

Le plan "d'antisymétrie" entre A et B : appelons-le CDEF

Les quatre sommets de ce plan sont au même potentiel et peuvent donc être réunis par des conducteurs sans résistance, sans modification de la résistance équivalente.

Il reste en conséquence
. 4 résistances en parallèle entre A et le plan : résistance R/4
. 4 résistances en parallèle entre le plan et B : résistance R/4

Ces deux résistances équivalentes sont en série, donc la résistance totale équivalente est 2(R/4) = R/2

Bonjour,

J'ai le même sujet, je trouve bien le même résultat mais la deuxième question de l'exercice me demande de calculer la valeur entre C et D, je ne comprend pas la méthode de résolution pour ce cas là..
Quelqu'un peu t'il m'aider ?

Merci.