Inscription / Connexion Nouveau Sujet
Eléctrocinétique complexe (RSF)
Bonjour,
Tout d'abord très bonne année 2013 à vous tous  .
.
Malheureusement, il faut très vite se remettre des fêtes pour rester dans le bain, c'est pourquoi j'aurais besoin d'un peu d'aide.
Le chapitre d'éléctrocinétique utilisant les notations complexes me pose quelques problèmes, ce sont les premiers exercices que j'ai à faire dessus, et j'ai un peu de mal.
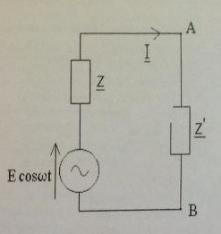
** énoncé effacé ; image laissée **
Je ne vois pas vraiment ce que l'on veut comme résultat pour l'amplitude complexe de la fém du générateur. D'après moi, ce serait simplement E = E e^(j*phi) mais je ne pense pas que ce soit si facile.. Si ?
Pour l'amplitude complexe du courant par contre, je pense avoir trouvé, voilà ce que j'ai noté :
I= E / Zeq
et Zeq = Z+Z' ce qui, d'après l'énoncé, nous donne :
Zeq = r+r'+j(x+x')
D'où :
I= E/[r+r'+j(x+x')]
Si mon premier résultat concernant E est juste, j'aurais donc :
I = E e^(j*phi)/sqrt[(r+r')2+(x+x')2]
Et la question 1 serait alors terminée.
Est-ce que c'est juste ? Si non, comment faire ?
En ce qui concerne les questions 2 et 3, je n'ai pas encore cherché.
Merci d'avance à tout ceux qui prendront la peine de lire, et de répondre 
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]()
Vraiment personne ne sait me dire si c'est juste ou faux ?
Je voulais d'ailleurs ajouter une petite modification concernant l'écriture de I qui serait plutôt, je pense :
I = E /sqrt[(r+r')2+(x+x')2]
Dans la suite, on me demande d'exprimer la puissance moyenne P' consommée par z', j'ai noté :
P' = U*I*cos(phi), en remplaçant tout simplement I par la valeur précédente, mais dois-je aussi donner une expression de U ?
Par ailleurs, la troisième question me bloque totalement, je n'ai rien répondu du tout.
On a z = r+jx et z'=r'+jx' comme tout à l'heure. On me demande quelle valeur de x' permettrait de maximiser la puissance moyenne consommée par z'puis, en supposant que x' a cette valeur, de déterminer la valeur de r' pour que P' soit maximale et de déterminer P'max.
Je ne vois pas du tout quelle peut être cette valeur x'...
Help 


