Inscription / Connexion Nouveau Sujet
Électrocinétique
Bonjour, svp j'ai besoin d'aide
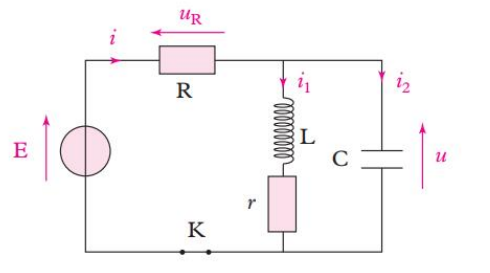
On donne le circuit ci dessous en régime permanent continu lorsque l'interrupteur K et ouvert à un instant choisi comme origine des temps.
On me demande de déterminer les valeurs des différentes grandeurs électriques juste après l'ouverture de l'interrupteur ainsi que les valeurs de ,
Je ne comprends pas comment utiliser le fait qu'on dise après l'après l'ouverture de l'interrupteur. J'ai pensé à trouver tout d'abord la loi d'évolution du courant principal lorsque l'interrupteur est fermé mais je ne sais si c'est utile pour la suite. Je me pose aussi des questions s'il y a continué entre 0- et 0+ pour les potentiels et courants du circuit. Là encore je ne sais pas comment me servir de ce résultat.
Bonjour,
La piste de la continuité est la bonne et pour écrire une relation de continuité, il faut bien savoir ce qui se passe avant ouverture. Il faut donc :
1- traduire "régime permanent continu" pour déterminer les tensions et courants juste avant ouverture.
2- écrire les relations de continuité.
En regime permanent continu, je pense que la bobine se comporte comme un 1)interrupteur fermé et le condensateur comme un interrupteur ouvert.
2) Je ne sais pas comment les écrire.
Pour 1) OK
Pour 2), pour chaque grandeur continu g(t=0-)=g(t=0+)
(t=0-) correspond au 1
(t=0+) correspond au "juste après l'ouverture de l'interrupteur"
Quelles sont les grandeurs continues dans le cas présent ?
À cause de 1) la branche contenant le condensateur peut être supprimée. On a i=i1=E/(R+r) à t=0-.
Je ne sais pas comment déterminer les grandeurs continues.
OK pour i=i1=E/(R+r). Pour la suite, il faut aussi u.
Les grandeurs continues c'est du cours, par ex. 
milieu page 3 et page 5
On voit d'après la continuité que i1(0+)=E/(r+R) et u(0+)=rE/(r+R). D'après la loi des mailles appliquée à t=0+, uL+ur+uR=E. Donc uL=E-(r+R)i(0+)=0. On a finalement=0
Je ne vois pas comment trouver
OK pour di1/dt
Dans le circuit avec inter ouvert, quelle est la relation entre i1 connu et du/dt cherché ?
À t=0-, u=ri1. Donc du/dt=rdi1/dt =0 car à t=0-, on est en régime permanent. J'émets des réserves à déduire la valeur en 0+ car rien ne me montre que du/dt est continue.
Oui, mais on veut à t=0+.
Pour t>0, en suivant le schéma, i1=-i2 et i2 est le courant de charge d'une capacité ce qui le relie à du/dt
Annuler
connectez vous