Inscription / Connexion Nouveau Sujet
Électrocinétique
Bonjour,
Je bloque un peu sur un exercice d'électrocinétique.
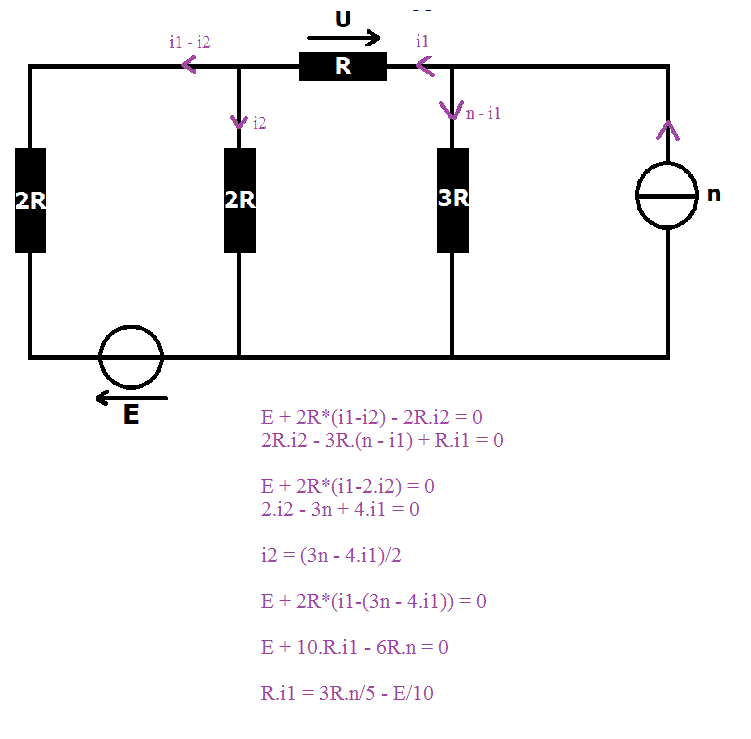
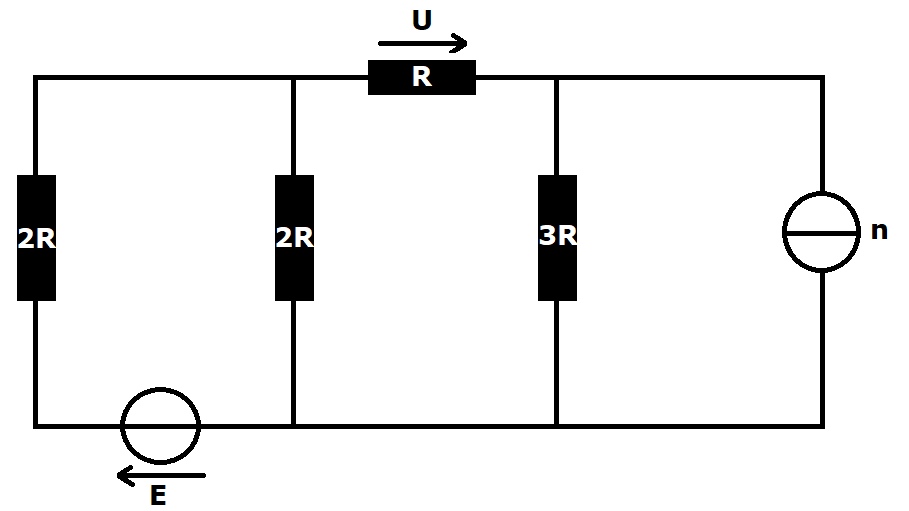
Le schéma est en pièce jointe. La question est : "Exprimer U en fonction de E, R et n"
J'ai essayé d'appliquer une méthode qui me donne un résultat qui dépend de E, R et n, mais je ne suis pas du tout sûr qu'elle soit juste.
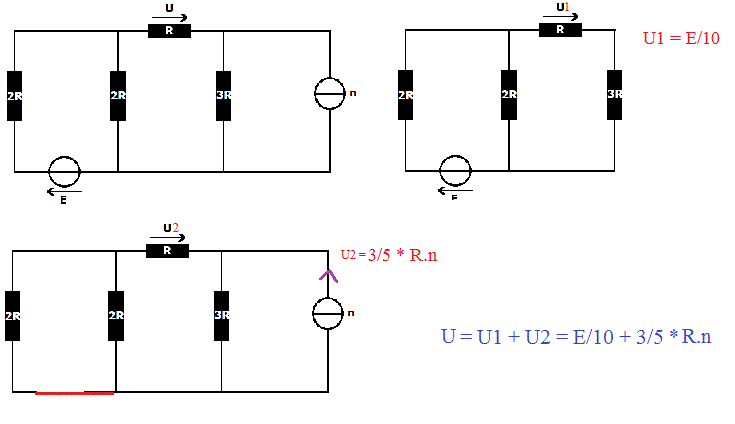
J'ai recopié le circuit sans n d'une part, et sans E d'autre part. J'ai donc deux circuits.
J'ai ensuite effectué des transformations Thévenin-Norton afin de simplifier les schémas, et j'ai pu calculer U dans chacun des circuits à l'aide du diviseur de tension.
J'obtiens alors deux résultats pour U, dont je fais la somme.
J'ai : U = (E/10) + (3Rn/5)
Pensez-vous que cette méthode est correcte ?
Si quelqu'un aurait la bonté de vérifier mon résultat, ça serait super sympa ! 
Merci d'avance.
Bonjour
La transformation Thévenin _ Norton permet assez simplement d'obtenir le résultat. En revanche, ton résultat est nécessairement faux car non homogène : une tension ne peut pas être égale à la somme d'une tension et d'une résistance !
Peux-tu un peu détailler ton raisonnement ?
Désolé : j'ai manifestement confondu la lettre grecque  avec un entier n. Si ton n désigne le courant électromoteur : pas de problème d'homogénéité !
avec un entier n. Si ton n désigne le courant électromoteur : pas de problème d'homogénéité !
Bonjour
La transformation Thévenin _ Norton permet assez simplement d'obtenir le résultat. En revanche, ton résultat est nécessairement faux car non homogène : une tension ne peut pas être égale à la somme d'une tension et d'une résistance !
Peux-tu un peu détailler ton raisonnement ?
n est une intensité (celle du générateur de courant à droite du schéma) donc, 3Rn est une tension non ? U = R.I
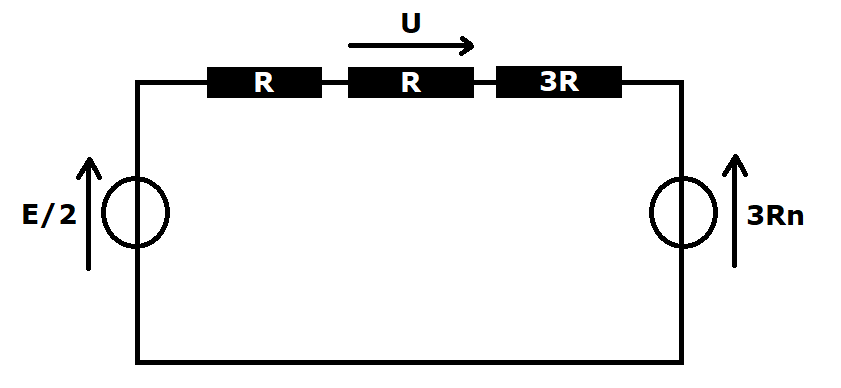
Après quelques transformations (veux-tu que je les détaille ? c'est assez long...), j'obtiens le schéma en pièce jointe.
J'enlève le générateur de tension 3Rn, j'applique le diviseur de tension.
J'obtiens U = (R * E/2) / (5R) = E/10
J'enlève le générateur de tension E, j'applique le diviseur de tension.
J'obtiens U = (R * 3Rn) / (5R) = 3Rn/5
Je viens de faire le raisonnement en utilisant la transformation Thévenin - Norton.
Tu ne précises pas le sens du courant électromoteur. Il est possible d'obtenir ton résultat mais, selon le sens de ce courant électromoteur, on peut être amené à placer un signe "-" devant le second terme.
Oui, je n'arrivais pas à écrire la lettre grecque alors j'ai remplacé par n.
Désolé, le schéma n'est pas parti.
Le voici :
Je viens de faire le raisonnement en utilisant la transformation Thévenin - Norton.
Tu ne précises pas le sens du courant électromoteur. Il est possible d'obtenir ton résultat mais, selon le sens de ce courant électromoteur, on peut être amené à placer un signe "-" devant le second terme.
Je suis tout à fait d'accord avec toi, mais le sens n'est malheureusement pas précisé dans le sujet (manque de rigueur surement), donc je l'ai choisi arbitrairement.
D'accord avec ton dernier montage. En supposant les deux flèches orientées vers le haut comme tu l'as fait, il y a un problème de signe...
D'accord avec ton dernier montage. En supposant les deux flèches orientées vers le haut comme tu l'as fait, il y a un problème de signe...
R est en convention générateur donc on devrait mettre un - dans le calcul avec le générateur E/2... C'est ça ? Donc -E/10 ?
Il manque le sens du courant du générateur de courant sur le schéma.
Si il est comme sur mon dessin ... alors, je trouve la même réponse que toi.
Sauf distraction. 
D'accord avec ton dernier montage. En supposant les deux flèches orientées vers le haut comme tu l'as fait, il y a un problème de signe...
... Il y a bien une erreur de signe sur la partie E/10 ... comme l'a indiqué Dumbledore

En effet, merci beaucoup à vous deux pour vos réponses !
Est-ce que vous voyez un autre moyen de résoudre l'exercice ?

On m'a dit que c'était faisable par la loi des nœuds et des mailles, mais je n'aboutis à rien du tout...
Quand tu peux éviter la loi des mailles, autant le faire ! Les lois de Kirchoff sont faciles à écrire mais ont l'inconvénient d'introduire dans le problème de nombreuses inconnues que les étudiants peinent ensuite à faire disparaître du problème. J'ai suffisamment d'expérience comme membre de jury de concours pour être en mesure d'affirmer que, sauf problèmes très simples évidemment, rares sont les étudiants qui se sortent correctement d'u,e situation un peu compliquée avec les lois de Kirchoff : beaucoup "tournent en rond" pour aboutir, après 20 lignes de calcul à quelque chose du genre I1+I2+I3=I1+I2+I3 (j'exagère à peine !) et les très rares qui s'en sortent ont passé tellement de temps sur la question qu'il n'obtiennent pas une bonne note globale à l'épreuve.
Les méthodes alternatives sont à préférer : diviseur de courant ou de tension, transformation Thévenin-Norton (la meilleure méthode ici à mon avis), théorème de Millman... Avec un peu plus d'expérience, tu trouveras vite la méthode qui te convient le mieux !