Niveau maths spé

Electrocinétique

Posté par
Flewer47 11-08-16 à 15:57

Bonjour,

Voici un exercice sur lequel je bloque :
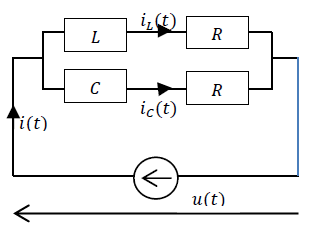
On considère le circuit suivant:
1) Pour quelle valeur $C_0$ de $C$ , $i(t)$ et $u(t)$ sont en phase indépendamment de la fréquence?
2) Pour $C=C_0$ , comparer les phases de $i_C(t)$ et de
$i_L(t)$ . Pour quelle valeur $\omega =\omega _0$ ces courants ont-ils même valeur efficace ?

Pour la 1), en disant qu'il faut $\underline{Z_eq}\in \R$ , j'obtiens $(R^2+L^2\omega ^2+R^4C^2\omega ^2+R^2C^2L^2\omega ^4)(L\omega +LR^2C^2\omega ^3-R^2C\omega -CL^2\omega ^3)=0$ .
La raisonnement suivant convient-il ?
Physiquement, le premier facteur ne peut être égal à 0.
On a dont équivalence à $L\omega +LR^2C^2\omega ^3-R^2C\omega -CL^2\omega ^3=0$ . On veut cela pour toute fréquence, donc il faut $L=R^2C$ i.e. $C_0=\frac{L}{R^2}$ . Réciproquement, avec cette valeur de $C$ , on a bien $L\omega +LR^2C^2\omega ^3-R^2C\omega -CL^2\omega ^3=0$ . Donc $C_0$ convient.

Pour la 2), je comprends que $\underline{Z_L}i_L(t)=\underline{Z_C}i_C(t)$ , mais comment faire pour la suite ?

Merci pour votre aide !

Electrocinétique

Posté par re : Electrocinétique 11-08-16 à 23:18

Bonsoir
Ni l'énoncé que tu as copié ni le schéma ne précise que le circuit est étudié en régime sinusoïdal établi. Cependant, compte tenu des questions posées, je vais faire comme si !
Pour la 1°, j'obtiens le même résultat que toi mais je me demande si tu ne t'es pas un peu compliqué la vie au niveau des calculs...

$\underline{Z_{e}}=\frac{\underline{Z_{1}}\cdot\underline{Z_{2}}}{\underline{Z_{1}}+\underline{Z_{2}}}=\frac{R^{2}+\frac{L}{C}+jR\left(L\omega-\frac{1}{C\omega}\right)}{2R+j\left(L\omega-\frac{1}{C\omega}\right)}$
i(t) et u(t) sont en phase si la partie imaginaire de $\underline{Z_{e}}$ est nulle. Ce qui revient à dire que le produit du numérateur par le conjugué du dénominateur doit avoir une partie imaginaire nulle.

$\Im_{m}\left\{ \left[R^{2}+\frac{L}{C}+jR\left(L\omega-\frac{1}{C\omega}\right)\right]\cdot\left[2R-j\left(L\omega-\frac{1}{C\omega}\right)\right]\right\} =0$
Soit :

$\left(L\omega-\frac{1}{C\omega}\right)\cdot\left(R^{2}-\frac{L}{C}\right)=0$
Puisque seule la solution indépendante de la pulsation est à prendre en compte, on obtient bien la valeur :

$C=C_{0}=\frac{L}{R^{2}}$
Pour la deux, je choisis de poser :

$u(t)=U\sqrt{2}\cos\left(\omega t\right)\quad;\quad i_{L}(t)=I_{L}\sqrt{2}\cos\left(\omega t-\varphi_{L}\right)\quad;\quad i_{C}(t)=I_{C}\sqrt{2}\cos\left(\omega t-\varphi_{C}\right)$
Sans ces précisions, il y a ambiguïté sur les signes des déphasages. Ici, $\varphi_{L}$ désigne clairement la différence (phase de u(t) - phase de i(t)) c'est à dire le déphasage de u(t) par rapport à iL(t) et non l'opposé. Même remarque pour $\varphi_{C}$ ...

Revois bien ton cours sur les complexes associés aux grandeurs sinusoïdales. Je fais le raisonnement seulement pour l'impédance $\underline{Z_{1}}$ de la branche {L,R} :

$\underline{Z_{1}}=\frac{\underline{u}}{\underline{i_{L}}}=\frac{U\exp\left(j\omega t\right)}{I_{L}\exp\left(j\left(\omega t-\varphi_{L}\right)\right)}=\frac{U}{I_{L}}\exp\left(j\varphi_{L}\right)$
Ainsi :

$|\underline{Z_{1}}|=\frac{U}{I_{L}}\quad et\quad\varphi_{L}=Arg\left(\underline{Z_{1}}\right)$
Conséquence : pour comparer les deux phases, il suffit de comparer les arguments des deux impédances complexes.
Pour comparer les valeurs efficaces, il suffit de comparer les modules des impédances complexes.

Posté par re : Electrocinétique 12-08-16 à 10:07

2)

Z1 = R + jwL
Z2 = R + 1/(jwCo) = (1+jwRCo)/(jwCo) = (1+jwL/R)/(jwL/R²) = R.(R + jwL)/(jwL) = (R/(wL)) * (wL - j.R)

arg(Z1) = arctg(wL/R) (mod 2Pi)
arg(Z2) = arctg(-R/(wL)) (mod 2Pi) (puisque wL positif)

Or f(x) = arctg(x) - arctg(-1/x) = arctg(x) + arctg(1/x) = Pi pour tout x > 0

Et donc arg(Z1) - arg(Z2) = Pi (mod 2Pi) (puisque wL/R > 0 (w = 0 interdit))

--> iC(t) et iL(t) sont en opposition de phase. (pour tout w différent de 0)
---
|Z1|² = R² + w²L²
|Z2|² = (R²/(wL)²) * (R² + w²L²)

|Z1| = |Z2| si R/(wL) = 1, don,c pour w = R/L

et donc wo = R/L
-----
Sauf distraction.

Posté par re : Electrocinétique 12-08-16 à 10:38

Merci bien Vanoise !
J-P : Presque tout est juste, sauf que les courants sont en quadrature. En effet, les formules sont : $\forall x\in {\mathbb {R} _{+}^{*}},\ {\arctan }\ {\frac {1}{x}}+{\arctan }\ x={\frac {\pi }{2}} \\ {\displaystyle \forall x\in {\mathbb {R} _{-}^{*}},\ {\arctan }\ {\frac {1}{x}}+{\arctan }\ x=-{\frac {\pi }{2}}}$

Posté par re : Electrocinétique 12-08-16 à 11:19

Fichtre, ce n'était pourtant pas l'heure de l'apéro.

Oui, arg(Z1) - arg(Z2) = Pi/2

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Electrocinétique

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique