Inscription / Connexion Nouveau Sujet
Electrocinétique 2
Bonjour,
J'ai du mal à faire cet exercice :
1) Donner les résistances d'entrée et de sortie du
quadripôle . La résistance d'entrée est donnée par
le rapport , expression qui ne dépend ni de
, ni de
, la résistance de sortie est donnée par la relation
, expression qui ne dépend pas de
.
2) Trouver le gain en tension c'est-à-dire le rapport .
Pouvez-vous m'expliquer en quoi ces rapports correspondent à ce que l'on demande, et comment faire pour les calculer ?
Merci d'avance !
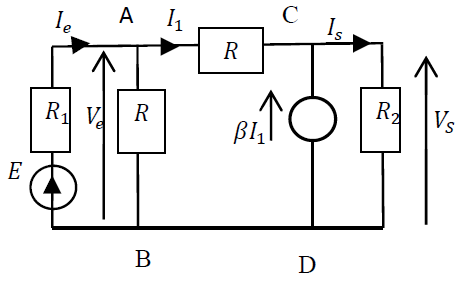
Par exemple pour la résistance d'entrée
Is = I1 + Beta.I1
Is = I1 * (Beta + 1)
Ve - R*I1 - Vs = 0
avec Vs = R2 * Is = R2 * I1 * (Beta + 1)
Ve - R * I1 - R2 * I1 * (Beta + 1) = 0
Ve = I1 * (R + R2.(Beta + 1))
Or Ie = Ve/R + I1
Ve = (Ie - Ve/R) * (R + R2.(Beta + 1))
Ve.(1 + (R + R2.(Beta + 1))/R) = Ie * (R + R2.(Beta + 1))
Ve.(2R + R2.(Beta + 1)) = Ie * R * (R + R2.(Beta + 1))
Ve/Ie = R * (R + R2.(Beta + 1))/(2R + R2.(Beta + 1))
Re = R * (R + R2.(Beta + 1))/(2R + R2.(Beta + 1))
----
Calculs non vérifiés.
Manipulations similaires pour Vs/Ve
...

Je trouve pareil effectivement.
Je n'arrive pas cependant pour le deuxième. Le de l'énoncé est-il le
du schéma ?
I1 = (Ve - Vs)/R
Is = (Beta + 1).I1
Is = (Beta + 1)*(Ve - Vs)/R
Vs = R2 * (Beta + 1)*(Ve - Vs)/R
R*Vs = R2 * (Beta + 1)*(Ve - Vs)
Vs*(R + R2 * (Beta + 1)) = Ve * R2 * (Beta + 1)
Vs/Ve = R2 * (Beta + 1) /(R + R2 * (Beta + 1))
-----
Es est la tension Vs lorsque Is = 0.
Es = lim(Is --> 0) Vs = lim(R2 --> +oo) Vs = Ve
Vs - Es = Ve * [R2 * (Beta + 1) /(R + R2 * (Beta + 1))] - Ve
Es - Vs = Ve * [1 - R2 * (Beta + 1) /(R + R2 * (Beta + 1))]
Es - Vs = Ve * [R + R2 * (Beta + 1) - R2 * (Beta + 1)] /(R + R2 * (Beta + 1))
Es - Vs = Ve * R/(R + R2 * (Beta + 1))
Rs.Is = Ve * R/(R + R2 * (Beta + 1))
Rs.Vs/R2 = Ve * R/(R + R2 * (Beta + 1))
Rs.Vs/Ve = R2 * R/(R + R2 * (Beta + 1))
Rs.R2 * (Beta + 1) /(R + R2 * (Beta + 1)) = R2 * R/(R + R2 * (Beta + 1))
Rs * (Beta + 1) = R
Rs = R/(Beta + 1)
-----
Calculs non vérifiés.

Je ne comprends pas très bien ce passage :
Es = lim(Is --> 0) Vs = lim(R2 --> +oo) Vs = Ve
Personnellement, d'après la loi des mailles, j'ai
Loi des mailles :
Ve - R.I1 = Vs
Or Is = (Beta + 1).I1
---> Ve - R.Is/(Beta + 1) = Vs
Et comme Es = Vs lorsque Is = 0, on a directement : Es = Ve
(Ne pas confondre Ve et E).
Ici, on s'intéresse à la tension d'entrée du quadripole (qui est Ve) puisque c'est ce quadripole qu'il est demandé de caractériser.
E est la force électromotrice du générateur attaquant le quadripole et R1 sa résistance interne (plus peut-être une résistance ajoutée), mais c'est sans importance ... puisqu'on ne s'intéresse dans les questions que du quadripole ABCD.



