Inscription / Connexion Nouveau Sujet
Électricité
Bonjour, pouvez-vous m'aider pour cet exercice svp 😊
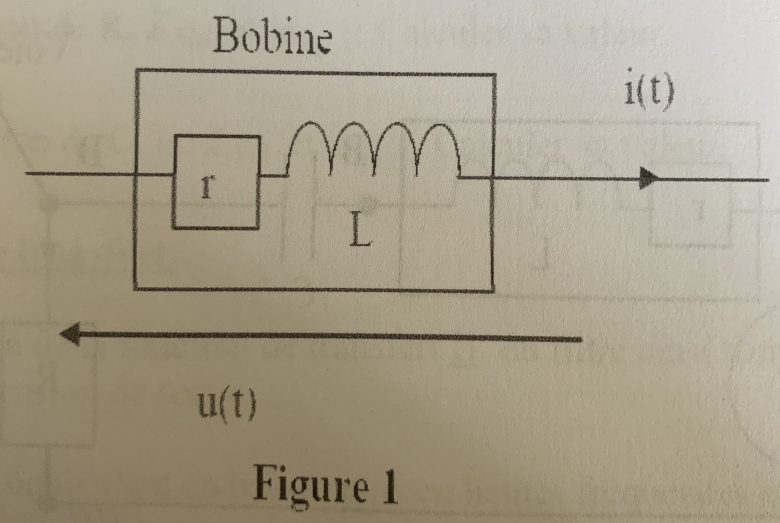
On dispose d'une bobine B que l'on assimilera à l'association série d'une inductance L et d'une résistance r. (L et r sont des constantes positives, indépendantes de la fréquence).
1) La bobine est parcourue par un courant i(t). Exprimer la tension u(t) à ses bornes en fonction de r, L, i(t) et de sa dérivée par rapport au temps.
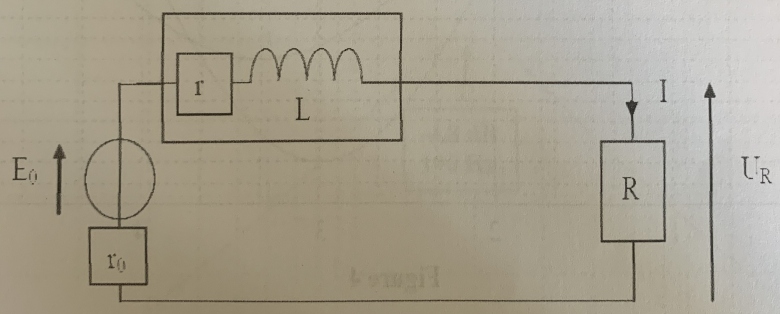
2) On réalise le circuit suivant en plaçant en série avec la bobine un resistor de résistance R=40
. L'alimentation est un générateur de tension continue, constante, de force électromotrice Eo = 1V et de résistance interne ro = 2
On mesure en régime permanent la tension Ur aux bornes de R. Exprimerai r en fonction des données de cette question. Calculer r avec Ur = 0,56V
Les schémas des circuits sont en pièces jointes.
Mes réponses :
U(t) = u(L) + u (r) = Ldi(t)/d(t) + r.i(t)
du(t) / dt = L.d2i(t)/dt2 + r.di(t)/dt
Je n'arrive plus ensuite... merci pour votre aide.
Bonjour
U(t) = u(L) + u (r) = Ldi(t)/d(t) + r.i(t)
OK ; cela suffit pour la question 1. L'expression de la dérivée de U(t) par rapport à t n'est pas utile ici.
Pour la question 2 : Puisqu'on étudie seulement le régime permanent , la tension aux bornes de la bobine est simplement : U=r.I ; la bobine se comporte en régime permanent comme une simple résistance r.
Pour obtenir Ur : deux méthodes possibles :
* la méthode directe consistant à remarquer que les différentes résistances en série se comportent comme un diviseur de tension vis à vis de la tension Eo ;
* la méthode consistant à déterminer d'abord l'intensité I du courant continu par application de la loi des mailles ou de la loi de Pouillet puis à écrire :
UR = R.I
Je te laisse continuer.
Merci pour vos réponses, est-ce L ou di/dt qui vaut 0 dans un circuit permanent ?
Eo = RI + rI
r = (Eo - RI )/I = (1-0,56)/??
Est-ce normal que je n'ai pas utilisé la valeur de ro? Je n'ai pas la valeur de I pour finir mon calcul....
Merci pour votre aide 🙂
Tu oublies ro.
Régime permanent : i ne dépend pas du temps. La dérivée par rapport au temps est nulle à chaque instant.
Merci, est ce correct si J'écris :
Eo + roI = RI + rI
r = (Eo +roI - RI )/I = (1-0,56)/??
Il me manque toujours le I pour les calculs....
Tu commets une erreur de signe :
Dans cette dernière relation, toutes les grandeurs sont connues sauf r...
Ah merci 😊
Ur (R + r + ro) = R.Eo
r = ( R.Eo - Ur.R - Ur.ro )/Ur = (1x40 - 0,56x40 - 0,56x2 )/0,56= 16,48 /0,56 = 29,4
Est-ce exact ?
Je poste la suite de l'exercice :
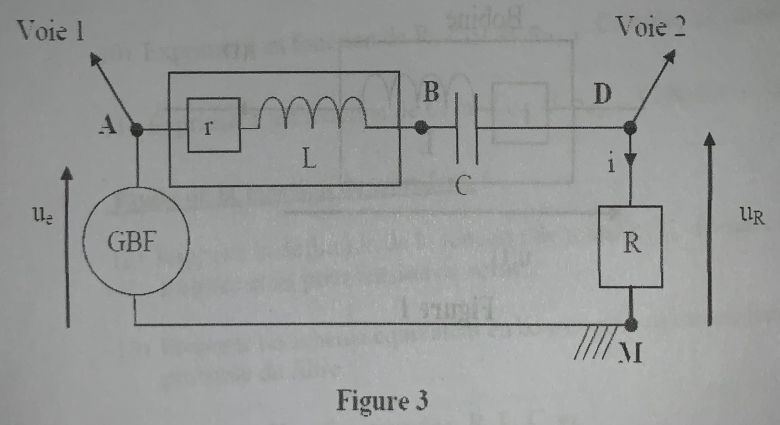
On place en série avec la bobine un résistor de résistance R=40 et un condensateur de capacité C = 10
F. Le GBF est réglé pour délivrer une tension sinusoïdale de fréquence f=250Hz et de valeur crête à crête de 10V. Deux tensions sont visualisées sur un oscilloscope numérique.
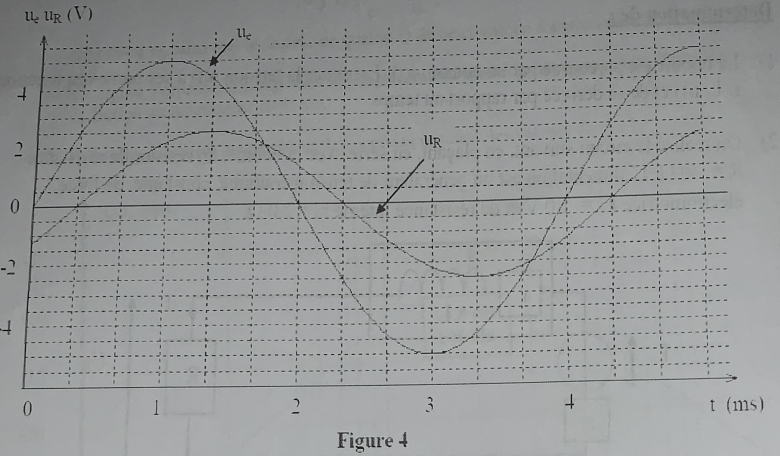
3) Déterminer l'amplitude Ue de la tension ue et l'amplitude Ur de la tension ur.
4) Déterminer l'amplitude I du courant i.
5) Rappeler l'expression générale de l'impédance Z d'un dipôle quelconque (module de l'impédance complexe). Calculer alors l'impédance Zam du dipôle AM.
6) Des deux tensions ur(t) et ue(t) laquelle et pourquoi d'après l'oscillogramme est en avance sur l'autre?
Mes réponses :
3) Ue = 6V et Ur = -2,5V
4) comment faire?
Merci 😊
D'accord avec ta valeur de r.
Pour la question 4 : il suffit d'appliquer la loi d'Ohm à la résistance R.
Merci
donc I = U/R = -2,5/40 = -0.0625A
5) L'impédance électrique mesure l'opposition d'un circuit électrique au passage d'un courant alternatif sinusoïdal. La définition de l'impédance est une généralisation de la loi d'Ohm au courant alternatif. On a Z= U/I avec U et I de formes sinusoïdales.
Zam du dipôle AM = -2,5/-0.0625A = 40
6) ur(t) est en avance sur ue(t) car le maximum est atteint pour ur(t) pour 1.33ms et pour ue(t) pour 1ms.
Merci pour votre aide 
Non. Dans cette partie, les lettres minuscules désignent les valeurs instantanées et les lettres majuscules les amplitudes c'est à dire les valeurs maximales.
Ainsi : UR=2,5V ; Ue = 5,0V
Non : il faut reprendre tes calculs en corrigeant les valeurs des amplitudes comme déjà indiqué.
Sinon, pour 6, je te pose une question : Plus la date d'un évènement est une valeur importante, plus l'évènement se produit tardivement. Quelqu'un arrive à l'école à 13h; quelqu'un d'autre arrive à 13h33 ; lequel dès deux arrive en avance par rapport à l'autre ?
Ah oui mince, celui qui arrive à 13h qui est en avance.
Donc:
5) Z= U/I => Zam du dipôle AM = 2,5/-0.0625A = - 40
6) ue(t) est en avance sur ur(t) car le maximum est atteint pour ur(t) à 1.33ms et pour ue(t) à 1ms.
Est-ce juste? merci
4) I = U/R = 2,5/40 = 0.0625A
5) Z= U/I => Zam du dipôle AM = 2,5/0.0625A = 40
6) ue(t) est en avance sur ur(t) car le maximum est atteint pour ur(t) à 1.33ms et pour ue(t) à 1ms.
Est-ce juste? merci
L'amplitude est la valeur maximale ; elle ne peut en aucun cas être négative dans le cas d'une grandeur sinusoïdale. Ce n'est pas la valeur à la date t=0 ! Je t'ai d'ailleurs indiqué les valeurs hier à 17h32. Une résistance ne peut être négative dans ce contexte, pas plus qu'une impédance !
OK pour 4)
Pour 5 : on demande l'impédance entre A et M ; il faut donc faire le calcul à partir de l'amplitude de la tension entre A et M soit Ue = 5V
Avec ta méthode, tu obtiens la valeur de la résistance R !
Ok,
5) Z= U/I => Zam du dipôle AM = 5/0.0625A = 80
Suite du sujet:
7) Déterminer précisément, à partir de l'oscillogramme, le déphasage 
ue,i entre ue et i (c'est à dire entre ue et ur).
8) Ecrire l'expression générale de l'impédance complexe Zam en fonction de r, R, L,C, 
9) Ecrire l'expression de l'impédance complexe Zam en fonction de son module Zam et du déphasage ue,i
10) Exprimer r en fonction de R, Zam et ue,i . Calculer sa valeur.
11) Exprimer L en fonction de C, , Zam et ue,i . Calculer sa valeur.
12) Rappeler la définition de la fonction de transfert H"barre" du filtre ainsi formé avec ue pour tension d'entrée et ur pour tension de sortie.
13) Proposer un schéma équivalent en basses puis en hautes fréquences et en déduire la nature probable du filtre.
14) Exprimer H"barre" en fonction de r, R, L, C,
15) Mettre H"barre" sous la forme H"barre" = Hmax/(1+j.Q.((/0) -(0/)).
On exprimera littéralement Hmax, le paramètre 0 ainsi que le facteur de qualité Q de ce circuit en fonction de r, R,L et C.
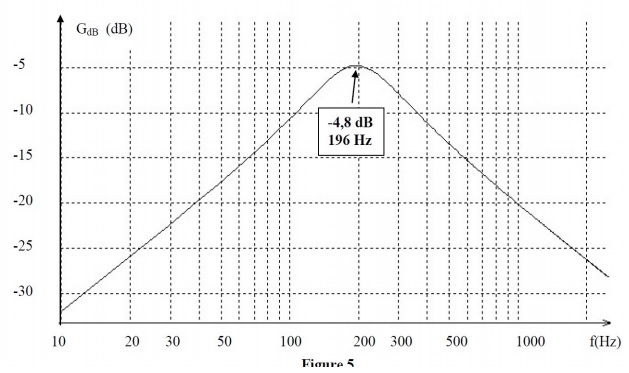
16) La figure 5 représente (en partie) le diagramme de Bode du filtre précédent. Rappeler la définition du diagramme de Bode.
17) Déterminer, à partir du graphe et des données initiales, les valeurs de r et L.
On reprend le montage figure 3 avec f=250Hz.
18) Rappeler la définition du facteur de puissance d'un circuit.
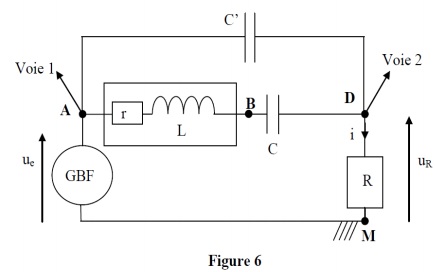
19) On place alors, en parallèle sur AD une boite de condensateurs à décades (figure 6) et l'on fait varier cette capacité C jusqu'à ce que en observant l'oscilloscope, ur et ue soient en phase.
Quelle est alors la valeur du facteur de puissance du circuit AM?
20) Quelle est alors la valeur du facteur de puissance du circuit AD?
21) Quelle particularité présente alors l'admittance complexe Y(AD) du circuit AD?
22) Exprimer Y(AD) en fonction de r, L, C, C' et de la pulsation
23) Déterminer C' en fonction de r, L, C, . Faire l'application numérique avec les valeurs de r et L calculées précédemment.
t/T)
360 = (-0,33/4)Concernant le déphasage, la valeur absolue peut être considéré comme correcte. On y arrive plus simplement en remarquant qu'un déphasage de 360° correspond à un décalage d'une période soit 12 divisions sur l'oscillogramme. Or le décalage correspond à 1 division sur l'oscillogramme. Cela donne donc un déphasage de (360/12)=30°.
Reste le problème du signe. L'énoncé demande de déterminer le déphasage de ue par rapport à i ; or ue est en avance par rapport à i.
Selon l'oscillogramme :
On pose en général :
Ainsi, le déphasage de ue par rapport à uR (ou de ue par rapport à i) est :
Par identification :
Ok merci 😊
8) Impédance complexe Z = R + j.X
Avec R partie réelle et X partie imaginaire.
Comment faire pour utiliser tous les termes dans la formule ?
Tu exprimes l'impédance complexe de l'association série (RrLC), tu exprimes l'impédance complexe de C' puis l'impédance complexe de l'association parallèle se calcule de façon analogue à ce qu'on fait pour les résistances en régime continu.
Si tu as des problèmes avec la manipulation des impédances complexes, tu peux étudier le document ci-dessous, du moins les six premières pages :
Annuler
connectez vous