Bonjour.
Tu as 6 inconnues : 3 tensions et 3 intensités.

On peut écrire une loi des noeuds, ainsi que deux lois des mailles (sur deux mailles différentes évidemment), ce qui donnera 3 relations indépendantes. On écrit en plus les 3 lois d'Ohm.
On a donc : 6 équations indépendantes pour 6 inconnues : on peut résoudre.

E1-R1.I1-R3.I3=0.........1
E2+R3.I3-R2.I2=0.........2
I1=I2+I3.................3
(3)remplace dans (1)    
E1-R1.(I2+I3)-R3.I3=0

((R2/R1)E1-E2)/(R3+(R2/R1)(R1+R3))=I3....... ?

Systèmes à 3 équations indépendantes 3 inconnues, pas de problème pour résoudre.

Je n'ai pas le courage de vérifier le calcul, mais ça m'a l'air bon.
Les résultats dans ce genre d'énoncé sont souvent lourds.

Si on veut vérifier rapidement la cohérence, il y a plusieurs choses à vérifier :
*S'assurer qu'il n'y a pas de différence au dénominateur, sinon cela voudrait dire que pour un choix arbitraires de valeurs de résistances, on aurait une intensité infinie, ce qui n'a pas de sens physique
*S'assurer que le comportement de l'intensité est cohérent en faisant tendre les valeurs de certaines résistances vers 0 ou l'infini.

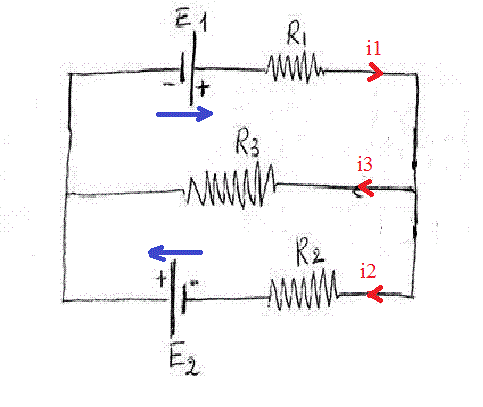
1)

i1 - i2 - i3 = 0
E1 - R1.i1 = R3.i3 = -E2 + R2.i2

E1 - R1.i1 = R3.(i1 - i2) = -E2 + R2.i2

R1.i1 + R3.i1 = E1 + R3.i2

i1 = (E1 + R3.i2)/(R1+R3)

R3.((E1 + R3.i2)/(R1+R3) - i2) = -E2 + R2.i2
R3.((E1 + R3.i2 - R1.i2 - R3.i2)/(R1+R3)) = -E2 + R2.i2
R3.((E1 - R1.i2)/(R1+R3)) = -E2 + R2.i2
R3(E1 - R1.i2) = (-E2 + R2.i2)(R1+R3)
i2(R1.R3 + R1R2 + R2R3) = E2(R1+R3) + R3.E1
i2 = (E2(R1+R3) + R3.E1)/(R1R3 + R1R2 + R2R3)

i1 = (E1 + R3.i2)/(R1+R3)

i1 = (E1 + R3.(E2(R1+R3) + R3.E1)/(R1R3 + R1R2 + R2R3))/(R1+R3)
i1 = [(E1.(R1R3 + R1R2 + R2R3) + R3.(E2(R1+R3) + R3.E1)]/[(R1R3 + R1R2 + R2R3)*(R1+R3)]
i1 = [(E1.(R1R3 + R1R2 + R2R3 + R3²) + E2.R3.(R1+R3)]/[(R1R3 + R1R2 + R2R3)*(R1+R3)]
i1 = [(E1.(R2(R1+R3) + R3(R1 + R3)) + E2.R3.(R1+R3)]/[(R1R3 + R1R2 + R2R3)*(R1+R3)]
i1 = [(E1.(R3 + R2) + E2.R3]/(R1R3 + R1R2 + R2R3)

i3 = i1-i2
i3 = [(E1.(R3 + R2-R3) + E2.(R3-R1-R3)]/(R1R3 + R1R2 + R2R3)
i3 = (E1.R2 - E2.R1)/(R1R3 + R1R2 + R2R3)

Et les tensions aux bornes des résistances par U = R.I
...
-----
i1 = (6*1200 + 12*1000)/(500*1000 + 500*200 + 200*1000) = 0,024 A
i2 = (12*1500 + 1000*6)/(500*1000 + 500*200 + 200*1000) = 0,03 A
i3 = (6*200 - 12*500)/(500*1000 + 500*200 + 200*1000) = -0,006 A
-----
3)

i3 = (E1.R2 - E2.R1)/(R1R3 + R1R2 + R2R3)
...

Sauf distraction.