Inscription / Connexion Nouveau Sujet
Ecoulement de Poiseuille
Bonjour, je fais un problème sur un écoulement de Poiseuille plan, et j'ai des difficultés à faire les dernières questions du problème (questions 6 où j'ai une piste et la 7 où je ne sais pas trop comment m'y prendre).
Voici l'énoncé :
On considère l'´écoulement stationnaire et laminaire d'un fluide incompressible (de masse volumique  = 10^3 Kg/m^3 et newtonien (de viscosité
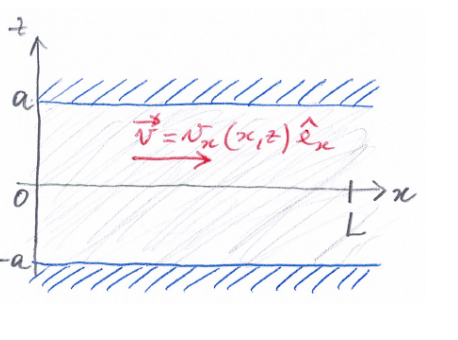
= 10^3 Kg/m^3 et newtonien (de viscosité  = 10 Pa.s) entre deux plans fixes situés aux hauteurs z = −a et z = a.
= 10 Pa.s) entre deux plans fixes situés aux hauteurs z = −a et z = a.
Le problème est analysé `a deux dimensions (x et z), entre les plans x = 0 et x = L et on néglige les phénomènes d'entrée et de sortie.
L'écoulement est généré par la différence de pression entre ces deux plans :
.
On donne également L = 0.5 m, a = 0.01 m.
Il y a une première partie où on aboutit à l'équation de la vitesse que je pense avoir réussi, et je trouve :
v = avec
.
Ensuite viennent les questions suivantes :
3) En supposant que l'écoulement a une largeur l = 0.1 m (dimension horizontale transverse à l'écoulement) donnez l'expression, puis la valeur numérique du débit volumique Qv.
J'ai trouvé : Qv = = 4.10^(-5) m^3/s.
4) Calculez la vitesse moyenne de l'écoulement (moyenne de vx(z) sur l'hauteur de l'écoulement).
J'ai fait Qv = S*v avec S = l*2a et j'ai trouvé 0,02 m/s.
5) Vérifiez que l'écoulement doit effectivement être considéré comme visqueux.
En calculant le nombre de Reynolds, on trouve 1.
6) Déterminez le vecteur force total de friction visqueuse exercée par le fluide en écoulement sur les deux parois horizontales, en fonction de , l et a.
Ici, je ne sais pas trop quoi faire, j'ai dF =  (
()dS (en vecteur) mais je ne sais pas comment utiliser cette équation (je ne comprends pas quelle vitesse ni la surface qu'il faut prendre en compte).
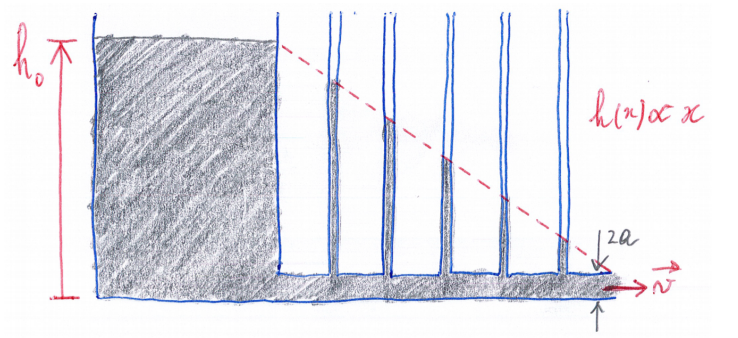
7 ) On rajoute à l'écoulement précédent un réservoir en amont, où on maintient l'hauteur du
liquide fixe, h0. On connecte à de différentes positions x, des tubes très fins en contact avec l'écoulement par leurs extrémités inférieures. Leurs autres extrémités sont ouvertes.
Dans la situation des questions précédentes (écoulement permanent) les tubes se remplissent à une hauteur fixe h(x) qui varie linéairement en fonction de la distance x du tube respectif au réservoir.
a) Pourquoi souhaite-t-on conserver la hauteur du réservoir constante ?
b) Comment s'explique le résultat schématisé par la figure ? Trouver la constante de proportionnalité entre h(x) et x
c) Comment peut-on utiliser un tel dispositif pour mesurer la viscosité dynamique ?
Pour la question 6), en fait je pense avoir trouvé (j'ai utilisé une formule ici ) et j'ai 2\Delta Pal
Force dirigée selon x.
Je n'arrive pas à trouver de réponses pour la question 7, auriez-vous une piste à me donner ? (surtout pour la 7.b)


