Niveau école ingénieur

Écoulement à surface libre

Posté par
Physical111 05-06-24 à 10:41

Bonjour à tous
J'ai un exercice merci beaucoup d'avance
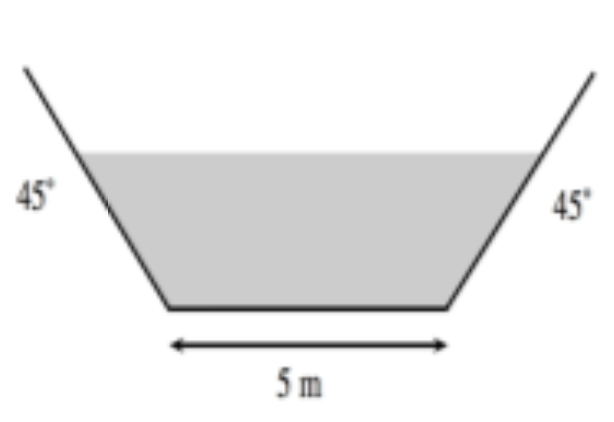
•Un écoulement d'eau en régime permanent uniforme se fait à travers un canal trapézoïdal de largeur à la base 5 m et dont les parois sont inclinées de 45° (voir Figure). La hauteur d'eau est de 4 m. La rugosité du lit est décrite à l'aide d'une relation de Manning-Strickler avec un coefficient K = 40 m^1/3/s.
1- Quelle est la largeur au miroir?
2- Quelle est la section d'écoulement ?
3- Quelle est la pente pour que le débit fasse 100 m³/s?
4- Quelle est la hauteur critique ?
5- Calculer le nombre de Froude. Dans quel régime d'écoulement est-on (super ou sub-critique)?
Écoulement à surface libre
Données de base :
- Largeur à la base, $b = 5 \, \text{m}$
- Hauteur de l'eau, $h = 4 \, \text{m}$
- Inclinaison des parois, $\theta = 45^\circ$
- Coefficient de Strickler, $K = 40 \, \text{m}^{1/3}/\text{s}$
- Débit, $Q = 100 \, \text{m}^3/\text{s}$ (pour la question 3)
1. Largeur au miroir
La largeur au miroir $ B $ se calcule en tenant compte de l'inclinaison des parois :
$[ B = b + 2h \tan(\theta)] [ \theta = 45^\circ \Rightarrow \tan(45^\circ) = 1 ] [ B = 5 \, \text{m} + 2 \times 4 \, \text{m} \times 1 = 5 \, \text{m} + 8 \, \text{m} = 13 \, \text{m}]$

2. Section d'écoulement
La section d'écoulement $ A $ d'un canal trapézoïdal est donnée par :
$[ A = h \left(b + \frac{B}{2}\right)] [ A = 4 \, \text{m} \left(5 \, \text{m} + \frac{13 \, \text{m}}{2}\right)] [ A = 4 \, \text{m} \left(5 \, \text{m} + 6.5 \, \text{m}\right) = 4 \times 11.5 = 46 \, \text{m}^2]$

3. Pente pour un débit de 100 m³/s
La formule de Manning-Strickler est :
$Q = K \cdot A \cdot R^{2/3} \cdot S^{1/2}$
où :
- $ R $ est le rayon hydraulique
- $ S $ est la pente du canal

Le rayon hydraulique $ R $ est donné par :
$R = \frac{A}{P}$
où $ P $ est le périmètre mouillé.
Le périmètre mouillé $ P $ est :
$[ P = b + 2h \sec(\theta)] [ \sec(45^\circ) = \sqrt{2}] [ P = 5 \, \text{m} + 2 \times 4 \, \text{m} \times \sqrt{2} = 5 + 8\sqrt{2} \approx 5 + 11.31 = 16.31 \, \text{m} ]$

Le rayon hydraulique $ R $ :
$\[ R = \frac{46 \, \text{m}^2}{16.31 \, \text{m}} \approx 2.82 \, \text{m}]\$
On substitue dans l'équation de Manning-Strickler pour trouver$ S $:
$[100 = 40 \times 46 \times (2.82)^{2/3} \times S^{1/2}]$
$[ 100 = 1840 \times 2.07 \times S^{1/2}]$
$[ 100 \approx 3808.8 \times S^{1/2}] [ S^{1/2} = \frac{100}{3808.8}] [ S = \left(\frac{100}{3808.8}\right)^2 \approx 6.89 \times 10^{-4}]$

4. Hauteur critique
La hauteur critique $ h_c $ pour un canal trapézoïdal se calcule à l'aide de la formule :
$h_c = \left( \frac{Q^2}{g \cdot B^2} \right)^{1/3}$
où :
- $ g $ est l'accélération due à la gravité, $g = 9.81 \, \text{m}/\text{s}^2$

$h_c = \left( \frac{100^2}{9.81 \times 13^2} \right)^{1/3} \approx \left( \frac{10000}{9.81 \times 169} \right)^{1/3} \approx \left( \frac{10000}{1657.89} \right)^{1/3} \approx (6.03)^{1/3} \approx 1.82 \, \text{m}$
5. Nombre de Froude
Le nombre de Froude $ Fr $ est donné par :
$Fr = \frac{V}{\sqrt{g \cdot h}}$
où $ V $ est la vitesse moyenne de l'écoulement.

La vitesse moyenne $ V $ :
$Q = A \cdot V \Rightarrow V = \frac{Q}{A} = \frac{100}{46} \approx 2.17 \ , \text{m}/\text{s}$
Le nombre de Froude :
$Fr = \frac{2.17}{\sqrt{9.81 \times 4}} \approx \frac{2.17}{\sqrt{39.24}} \approx \frac{2.17}{6.26} \approx 0.35$
Un nombre de Froude inférieur à 1 indique un régime d'écoulement subcritique.
Merci beaucoup d'avance