Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... MasterForum Supérieur de master PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau master
Partager :

Echanges Thermique

Posté par
QiRua 28-01-21 à 14:27

Bonjour à tous,

Je cherche à résoudre une équation différentielle qui simule un bilan thermique.
l'équation est la suivante:
C\times m \times \frac{dT}{dt}=R\times I^{2}-H\times S\times (T - T_{a})

C : capacité thermique massique
m : masse
R  : résistance électrique interne équivalente
I : intensité du courant en rms
H : coefficient de convection
S : surface d'échange
Ta :  la température ambiante

Si vous pouvez m'aider pour la résolution svp.

Posté par
vanoisere : Echanges Thermique 28-01-21 à 14:34

Bonjour
Tu as une équation différentielle du premier ordre à coefficients constants :


C\times m\times\frac{dT}{dt}+H.S=R\times I^{2}+H\times S\times T_{a}

Posté par
vanoisere : Echanges Thermique 28-01-21 à 14:35

Etourderie dans la formule ; je rectifie :

C\times m\times\frac{dT}{dt}+H.S.T=R\times I^{2}+H\times S\times T_{a}

Posté par
QiRuare : Echanges Thermique 28-01-21 à 15:38


Avec comme condition initiale : T(0)=Ta, j'obtiens :


T(t)=( Ta - \frac{R.I²+H.S.Ta}{H.S}) .\exp (\frac{-H.S.t}{C.m})+\frac{R.I²+H.S.Ta}{H.S}



Le but de cette résolution différentielle est maintenant de sortir le H de cette équation pour le déterminer, mais j'étais bloqué à ce niveau, c'est pourquoi j'ai reposé le problème depuis sa base pour voir si je n'ai pas une erreur quelque part.

Posté par
vanoisere : Echanges Thermique 28-01-21 à 15:48

Si tu as pu enregistrer la courbe T=f(t) avec un dispositif enregistreur quelconque, plusieurs méthodes sont possibles pour déterminer H . Tout dépend des grandeurs connues par ailleurs. On peut raisonner sur la constante de temps ; on peut aussi raisonner à partir de la valeur asymptotique...

Posté par
QiRuare : Echanges Thermique 28-01-21 à 16:01

J'ai effectué des mesures pour obtenir une courbe  T= f(t) et toutes les autres variables de l'équation sont connues.

Je voulais donc ressortir le H de telle sorte d'obtenir H= ....
De toute évidence, il est difficile d'obtenir sa valeur par cette méthode vu la complexité de l'équation.

Pouvez-vous plus me détailler vos deux raisonnements: sur la constante de temps et la valeur asymptotique SVP

Posté par
mmalou Webmasterre : Echanges Thermique 28-01-21 à 18:05

Bonjour à tous les deux,
QiRua, peux-tu renseigner ton profil s'il te plaît ?

attentionextrait de c_faq la FAQ du forum :

Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau topic ?


Merci

Posté par
vanoisere : Echanges Thermique 28-01-21 à 18:26

La solution de l'équation différentielle est de la forme :

T_{(t)}=A.exp\left(-\frac{t}{\tau}\right)+T_{\infty}

Avec :
\tau=\frac{C.m}{H.S} : constante de temps

T_{\infty}=\frac{R.I^{2}+H.S.T_{a}}{H.S}=\lim_{t\rightarrow\infty}T_{(t)} : ordonnée de l'asymptote horizontale à la courbe.

La détermination de l'ordonnée de l'asymptote horizontale permet donc de déterminer H si les autres constantes sont connues. A titre de vérification de la cohérence du modèle utilisé, tu peux représenter la courbe :

\ln\left(T_{(t)}-T_{\infty}\right)=g(t)

Si le modèle est correct, tu vas obtenir des points sensiblement alignés le long d'une droite de coefficient directeur \left(-\frac{1}{\tau}\right). La mesure de ce coefficient directeur permet de calculer la constante de temps et d'obtenir une nouvelle valeur de H que l'on peut comparer à celle obtenue à partir de l'asymptote.

Tu as aussi des logiciels qui permettent de tracer les courbes et de faire les calculs. Un simple tableur type LibreOffice ou Excel peut convenir. Certains logiciels scientifiques font aussi cela directement : Matlab, Scilab, Synchronie, Latis Pro, programme Python....

Si tu as des difficultés, tu peux poster ici ton tableau de mesures, en précisant, parmi les logiciels que j'ai cités, ceux que tu connais.
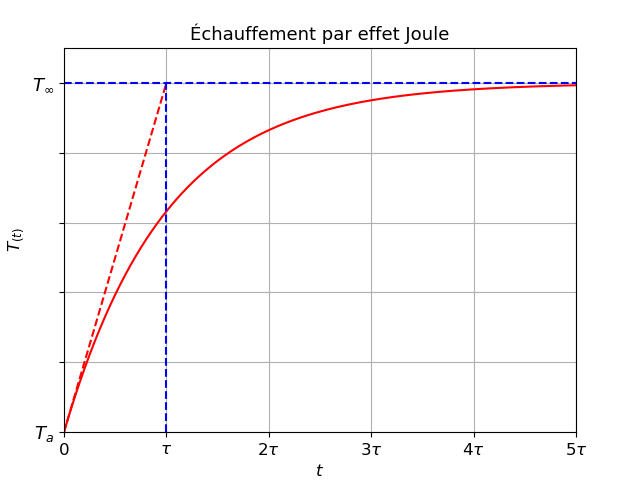
Voici l'allure de la courbe que tu devrais obtenir.

Echanges Thermique

Posté par
QiRuare : Echanges Thermique 29-01-21 à 08:57

Merci beaucoup pour toutes ces explications, je vais essayer de mon côté.

Je vous tiens au courant de mon avancée et je n'hésiterais pas à revenir vers vous en cas de difficulté.

Au niveau des logiciels, j'ai déjà pratiqué sur Scilab qui est gratuit, mais c'était que des applications élémentaires.

Posté par
QiRuare : Echanges Thermique 29-01-21 à 15:43

Voilà, pour mon retour, j'ai dans un premier temps trouvé l'asymptote et obtenu une première valeur de H.

C'est pour la vérification que je n'ai pas exactement suivi votre idée. En effet, pour la tangente, vous m'avez conseillé de tracer une tangente d'équation :

\ln (T_{(t)}-T_{\infty })=g(t)

Puis de déterminer son coefficient directeur pour obtenir une nouvelle valeur de H.

Le problème est que  T_{(t)}-T_{\infty } est forcément négatif... J'ai donc pas compris comment faire étant donné que la fonction ln n'est pas définit sur cet intervalle.
J'ai donc déterminé l'équation de la tangent autrement. Je suis revenue à l'équation différentielle initiale :

C.m.\frac{dT}{dt} = R.I² - H.S.( T - T_{A})

On remarque sur la courbe que dans les premières secondes l'expression est linéaire d'une forme T(t) = a.t + b.
Et physiquement, cela s'explique que la dissipation en température est négligeable. Et la dissipation dans le modèle, ce fait uniquement par convection, qui suit la loi de Newton H.S.ΔT. Si il y n'y a pas de dissipation c'est-à-dire ΔT=0.
On a donc:

C.m.\frac{dT}{dt} = R.I² \\ \\ Puis après intégration : \\ \\ [tex]T(t) = \frac{R.I²}{m.C}.t + T_{(t=0s)}

J'ai ensuite vérifié graphiquement, pour confirmer. Puis par identification, j'ai trouvé une seconde valeur de h avec la constante de temps.
Les deux valeurs obtenues sont quasiment égales à 0,0002 prêts.


En tous cas, je vous remercie pour votre précieuse aide.

Posté par
QiRuare : Echanges Thermique 29-01-21 à 15:45


Pour les erreurs il s'agissait de :

C.m.\frac{dT}{dt} = R.I²

Puis après intégration :

T(t) = \frac{R.I²}{m.C}.t + T_{(t=0s)}

Posté par
vanoisere : Echanges Thermique 29-01-21 à 18:28

Je commence par te présenter mes excuses : j'ai effectivement commis une étourderie. Il faut lire :

\ln(T_{\infty}-T_{(t)})=g(t)

Sinon, tu as raison, pour t<<, la courbe est assimilable à sa tangente à l'origine. Cela se démontre en effectuant un développement limité de l'exponentielle.

Si :

T_{(t)}=A.exp\left(-\frac{t}{\tau}\right)+T_{\infty}

Pour t<< :

T_{(t)}\approx A.\left(1-\frac{t}{\tau}\right)+T_{\infty}=-\frac{A}{\tau}\cdot t+\left(A+T_{\infty}\right)

Puisque A<0, cela te donne une droite de coefficient directeur positif. Il s'agit de la ligne en pointillés rouges de mon message du 28-01-21 à 18:26. Petite astuce pour déterminer facilement sans calcul. On démontre que cette droite coupe l'asymptote horizontale d'équation T=T à la date t=.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !