Bonjour.j'ai pas peu résoudre cet exercice qui représente le travail de recherche pour les étudiants.il est un peu long et je vous pries de m'aider en expliquant la procédure de réponse.

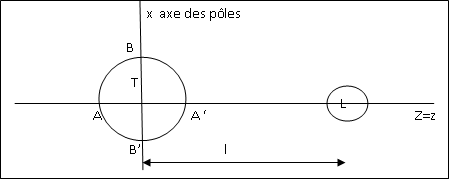
A,A,B,B' sont les points de la surface océanique.ces point vérifient la propriété suivante: Ep[A]=Ep[B] et  Ep[A']=Ep[B']. les points A et B sont situé sur l'équateur .leur longitudes différentes de 90°. l est très supérieur a R[T].
1- Établir l'expression de l'accélération @ dans le référentiel muni de la base (O,Y,Z)de la premier figure.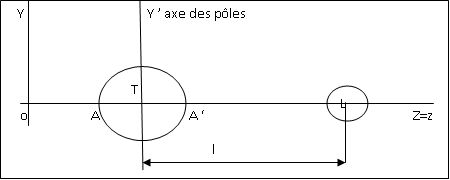
2-a  Établir l'expression d'un point M de la surface océanique dans le repère (T,Y,Z).
2-b soit les coordonnée de M(x,y,z) dans ce repère.établir l'expression exacte de l'accélération de M  dans le dit repère en expliquant les forces agissantes sur M.
3-a  on appelle F[eff] (c'est en vecteur) la quantité m@( ou @ est en vecteur). écrire les 03 composantes de F[eff] dans la base  i,j,k lié a(T,X,Z).
3-b établir les approximations qui s'impose en tenant compte dune part de la position de M(proche de la surface de la Terre)et de l très supérieur a R[T].
4-Calculons la variation d'énergie potentielle  Ep[eff] entre 2 point A et B proche de la surface Terrestre.
5-montrer que les 2 points A et A' symétrique par rapport  au plan xTy ont même énergie potentielle et donc même état de marée.
6-a calculons la différence d'énergie potentielle entre A(x=0,y=0, z=R[T]+u)et B(x=R[T],y=0,z=0)ou u est un infiniment petit par rapport a R[T].
6-b développer l'approximation au premier ordre en  u  de l'expression si dessus.
7-le niveau de B étant pris comme référence de marée basse,cherchez l'élévation  u  du niveau de la mer en A(marée haute).


je vous serais très reconnaissant d'avoir réponse a cet exercice.